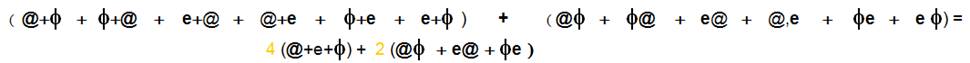02/09/2010

L’@lliance  : @

J’ai rencontré ce nombre sous 2 formes mathématiques :

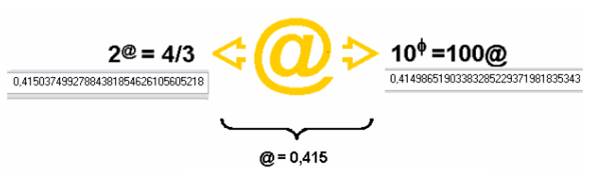
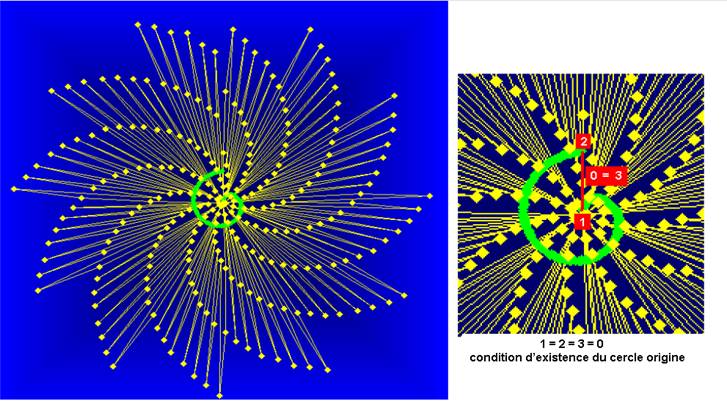
• La condition d’existence du cercle , la Fleur d’Or, a conduit à la première forme :2^@ = 4/3 . Elle entraînera une relation avec π, caractéristique du cercle.

Le cercle est la vision absolue d’une spirale qui peut se fermer dans la perfection :

.

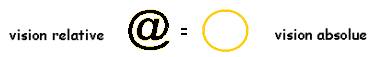• La 2^ème forme :10 ^φ =100@ est en lien avec le Nombre d’Or φ .

Ces 2 relations semblent à l’origine du logarithme à base 2 et du logarithme décimal ( à base 10) .

Elles se transforment respectivement :

Ces logarithmes trouvent ici un lien avec le nombre 2, qui apparaît comme vraiment spécial !... tout à fait irrationnel … ou transcendant … transcendant fini !... serait-ce une nouvelle définition du TRANSFINI ?

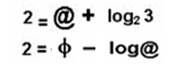
Ces 2 logarithmes son liés au logarithme népérien à base e .

Le logarithme trouve ici son origine, dans ce lien inattendu rationnel-transcendant

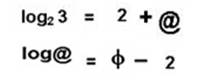
Ces relations lient φ @ et e (fonction réciproque du logarithme népérien)

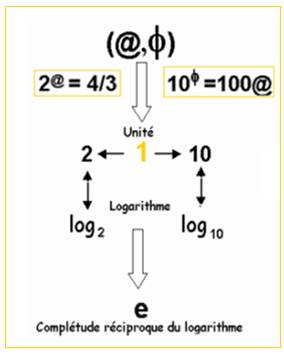
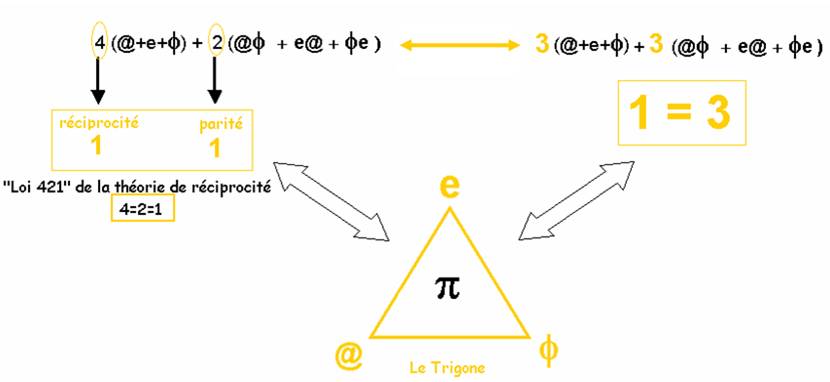
Je représente par un triangle ce lien, entre les 3 nombres transcendants (@ , e , φ), qui traduit la perfection absolue du cercle et son existence dans notre mathématique relative

C’est du cercle qu’ont été déduites les propriétés trigonométriques. Pourquoi « trigonométrique » ? (je ne l’ai jamais su)

Je découvre ce qu’est «  le TRIGONE  »  : ,

J’ai alors l’idée de calculer la somme @ + e + φ

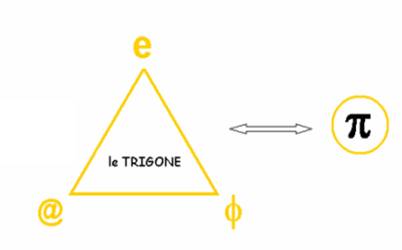
et de la comparer à π qui est caractéristique du cercle et utilisé dans les relations trigonométriques.

La différence

@+e+ φ- π =

m’apparaît comme la valeur du « mille anglais » !

Pour moi ce sera « l’unité trigonométrique ».

Que traduit-elle ? : Le lien de réciprocité des 4 nombres transcendants (@,e, π, φ ) :

Il existe un parfait échange entre eux qui crée leur unité  que j’écris 1:

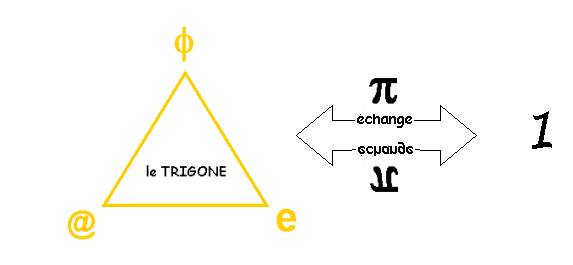
Le signe «  -  » dans la compréhension de cet échange-partage, n’a pas le sens arithmétique que nous avons l’habitude d’utiliser . L’échange se fait dans les 2 sens :

- vers l’extérieur (- π ),

- vers l’intérieur (+ π ) : alors l’unité des 4 peut être représentée par le symbole Cercle, Grand Contenant (forme du ZERO) :

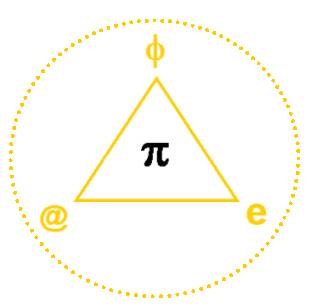
La représentation abstraite mathématique serait alors @ + e + π + φ = 0 ( 0 a un contenu !)

Par cet échange , chacun devient la totalité de la somme, leur unité 1.

L’échange est réciproque : il se fait dans les 2 sens . C’est une circulation dans les 2 sens : ce qui s’échange, qui circule est identique en tout point : trigone = π = 1

@ = e = π = φ = 1 s ‘écrira (@,e, π, φ ) = 1

- ( « Circulation ? »… quel est le sens de ce mot ?

- Les 2 sens sur le Cercle … trigonométrique ! )

On choisira donc des symboles circulaires pour représenter la réciprocité réversible de l’échange :

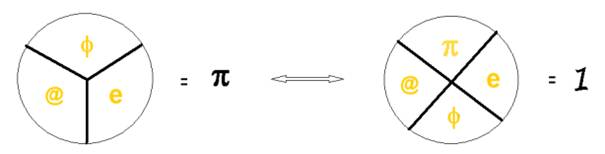
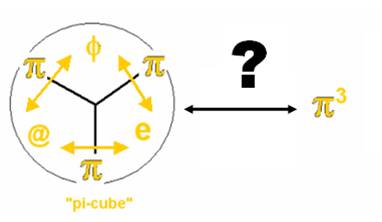
Ces symboles que j’ai introduits dans « la théorie de la réciprocité » sont équivalents :

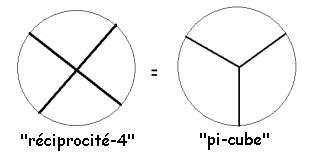
J’avais nommé, sans savoir pourquoi, mais d’une façon qui s’était imposée à moi avec force, « pi-cube » le symbole ternaire :

Il semble prendre ici tout son sens, car je vois l’échange de π entre les 3 nombres :

Par l’échange de p, le trigone devient UN.

Comme précédemment je vais comparer les 2 termes :

- La relation des nombres fait intervenir le contenant et le contenu, ce qui se traduit par la somme et le produit  comme je l’ai montré dans l’étude des nombres.

Ainsi la relation dans le trigone qui est la relation de 3 nombres s’exprimerait simplement par : 3 (@+φ+e) + 3 (@φ+ e@ + φe ) , une triple relation (somme et produits) entre 3 nombres

- On peut voir aussi cette relation dans le trigone comme l’échange réciproque entre les 3 constantes @,e, φ .

C’est un triple double échange :

Dans un couple réciproque , l’échange se fait à 2 niveaux , par l’addition (contenant) et le produit (contenu) , ce qui donne une représentation mathématique :

On peut donc représenter le trigone par 2 relations qui traduisent l’échange :

.Leur équivalence traduirait la validité et la complémentarité de 2 théories :

- la « théorie de la réciprocité » : 4 =2=1 (unité 4)

- la théorie du « relatif absolu » : 1 = 3 ( unité trine)

:

Avec une valeur approchée de @, le calcul numérique donne :

De la même façon :

· la valeur de @ :

Une valeur approchée a été utilisée pour trouver la valeur 13

Ayant cette égalité ou équation, il est possible de calculer la valeur de @ qui la construit :

-Cette valeur peut être utilisée de nouveau pour recalculer dans la formule… elle redonnera une autre valeur plus précise…

Ces valeurs sont par excès… on continue l’opération jusqu’à ce que l’on trouve la même valeur par des rapprochements successifs.

-On peut faire de même avec la deuxième formule qui donne les valeurs par défaut .

-Les 2 doivent tendre vers la même valeur.

Dans le prochain chapitre le sens des formules ci-dessus sera explicité

Suite OR-igine

00001-Chapitres