La table de multiplication et la fonction
logarithme
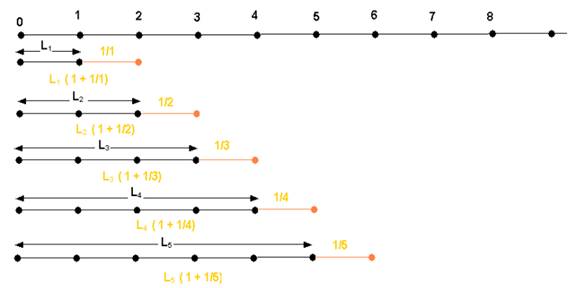
La suite des nombres 1, 2, 3, 4, 5… peut être représentée par les longueurs L 1, L 2, L 3, L 4, L 5 …
La relation entre 2 longueurs successives est de la forme : Ln+1= L n(1 + 1/n), comme le montre l’illustration ci-dessous :
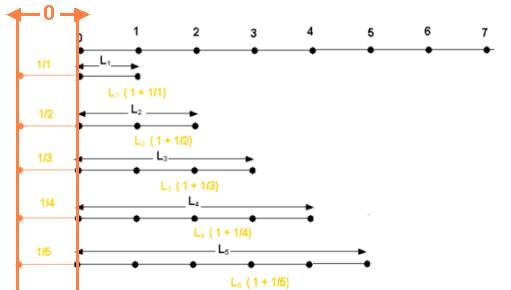
0n peut alors introduire une longueur « 0 », qui serait origine :
si nous considérons chacun des nombres n comme une longueur L . la longueur « 0 », dimension de l’origine est telle que pour chacun des nombres n, que nous considérons comme une longueur L :
0 = Ln/n =1
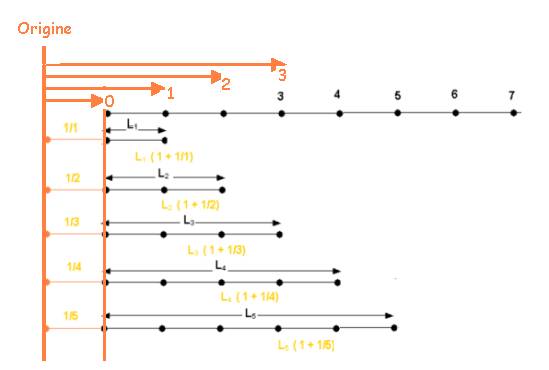
Le nombre sera représenté alors à partir d’une nouvelle origine « décalée »
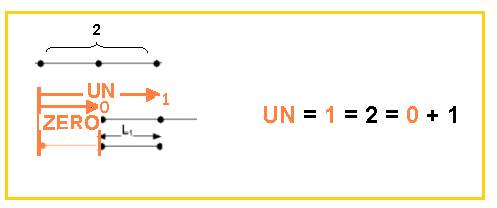
- La nouvelle unité, ou unité de complétude UN = 1, inclut le ZERO, et a la longueur L2 initiale = 2
- La
longueur Ln est la somme :
Ln = L 1/1 + L 2/2 + L3/3 + L4/4 +..... + Ln/n
Il lui correspond le nombre
n :
n = 1/1 + 2/2 +
3/3 + 4/4 +
…. + n/n
![]() n
= 1 +
1 + 1
+ 1 +
… + 1
n
= 1 +
1 + 1
+ 1 +
… + 1
nx1
On est passé ainsi de l’addition à la multiplication.
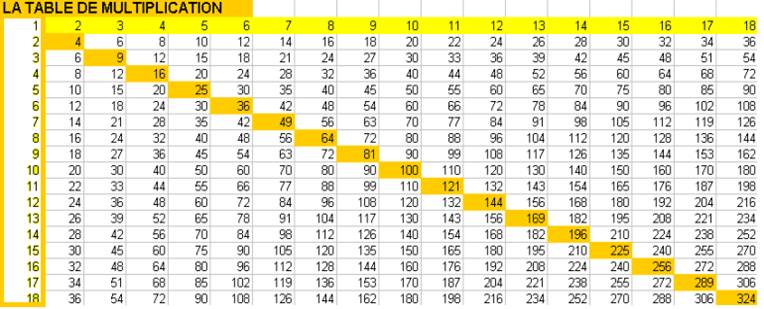
- La formule Ln+1= L n(1 + 1/n) = L n + L n /n. permet de tracer la table de multiplication, par un tableau d’addition
Il suffit de porter la formule dans chacune des colonnes d’un tableur :
Au départ on a la suite des nombres en colonne 1
Ici , la formulation du tableur Excel donne : (colonne n+1 ) = LC(-1)+LC(-1)/n
(colonne 3) =
LC(-1)+LC(-1)/2
(colonne 4) =
LC(-1)+LC(-1) 3
(colonne 5) =
LC(-1)+LC(-1)/4 …
- La fonction logarithme établit une relation entre nombre et longueur
![]()
Elle traduira la paradoxale relation entre nombre et
longueur : 0
= Ln/n =1 à partir de l’égalité
1=2
La relation entre le nombre et la longueur qui le représente, est la relation entre le nombre (contenant ou NOM) et son contenu qui peut se quantifier (1 +1 +1+1…+1).
Le logarithme exprime la relation contenant-contenu, c’est la relation paradoxale, réversible qui lie 0 et 1