Ils ne sont pas aléatoires :
Les nombres premiers prennent leur place…
NATURELLEMENT
… la première qui est libre !
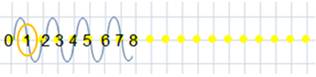
L’onde 1, le UN PREMIER, dans
sa propagation, éclaire progressivement tous les points de l’axe gradué, tous
les nombres N que nous connaissons : les entiers NATURELS.
J’utilise le verbe
« éclairer » en référence à une onde-lumière :
Les ombres, éclairées,
deviennent ‘No-ombres’, et se forme la suite NATURELLE des nombres N .
La nature duelle du nombre
s’écrit « Nombre&lumière »
Si nous écartons le cas bien
particulier du 1 :
Pour éclairer tous les points de
l’axe, il faut ajouter successivement des ondes-lumière :
On comble les trous, ombres,
en éclairant progressivement par l’onde-lumière 2, puis 3 :
J’ajoute
les ondes-lumière qui comblent, en
suivant, les places vides .
Ces
ondes définissent les nombres
premiers : la suite des nombres
premiers Pn se construit NATURELLEMENT...
,
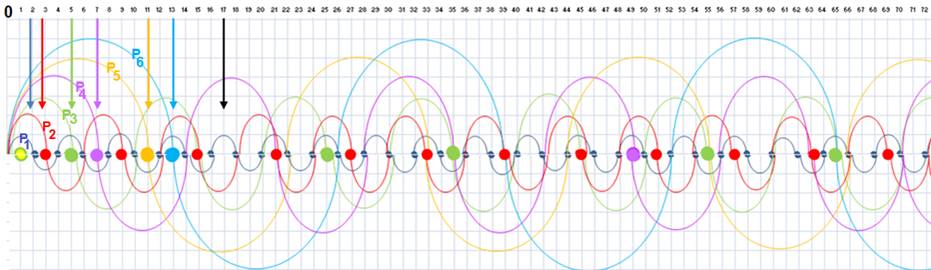
La
position des nombres premiers P1,P2 ,P3,P4,P5,P6…est
ainsi définie ,
ainsi apparaissent les nombres 2,3,5,7,11,13….
La
prochaine place vide, « ombre 17 »
deviendra le nombre premier 17, avec l’onde-lumière suivante.
Remarque:
les ondes 2,3,5,7,11,13 ont éclairé tous
les multiples de ces nombres jusqu’à 132 = 169, les ombres qutei
restent jusque là seront des nombres premiers, d’où la généralisation dans la
remarque suivante :
En traçant l’onde P suivante , on détermine tous les
nombres premiers inférieurs à P2 .
(on
fait une remarque analogue quand on utilise le crible d’Eratosthène)
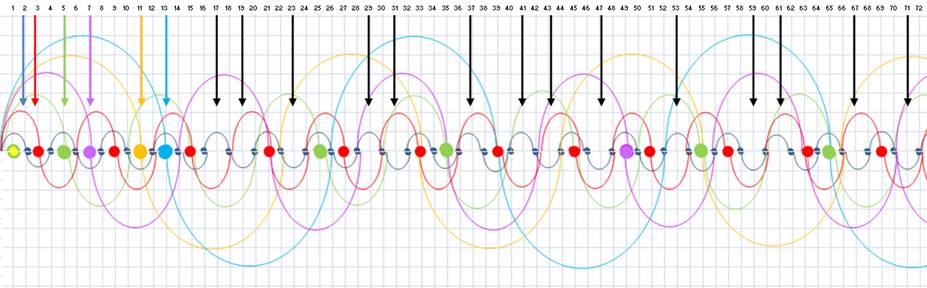
Ainsi dans l’image limitée ci-dessus, les ondes: 2, 5, 7 ,11, 13, laissent les
ombres 17 19 23
29 31 37 41 43 47 53 59 61 67 71.
Les ondes-lumière s’y formeront successivement … les nombres premiers y prennent leur PLACE
naturellement … et leur « NOM »
(Remarque : L’ajout successif des ondes ci-dessus pourrait révéler des ombres -
nombres premiers jusqu’à 712= 5041… :
on aurait la position et le nom des nombres premiers jusqu’à
5000…)
Conclusion ou la clé
de l’énigme des nombres premiers :
C’est la NATURE des nombres premiers,
leur NATURE-ONDE
qui révèle simplement, successivement, leur apparition qui semblait mystérieuse :
La distribution,
position, des nombres premiers est toute naturelle.
Il n’y a pas besoin de
démonstration mathématique pour le montrer, une étonnante simplicité cachait le
grand mystère des nombres
premiers !... un
enfant de CP peut trouver les nombres premiers jusqu’à 100, c’est un jeu d’enfant !
Il existe ainsi une relation très particulière entre la suite des entiers naturels et la suite naturelle des nombres
premiers :
Les
nombres premiers, vus comme des ondes, créent
et comblent progressivement…et infiniment… la liste des nombres N ! :
Les nombres
premiers génèrent nos nombres N.
Chaque nombre premier prend sa place…
NATURELLEMENT !...
la première place qui est libre…
…ceci permet « dans l’autre sens » la vision du crible d’Erathostène, crible des entiers N par les nombres
premiers :
mathématiquement
la liste infinie des nombres premiers s’écrira avec l’algorithme des nombres premiers dans le crible paradoxal.