La Boucle
Transfinie des Nombres
Description :
Les Nombres s’enroulent
en hélice sur un cylindre fermé en Tore
Une spire est une boucle à 12 points :
(Voici un schéma que je vais expliquer et justifier)
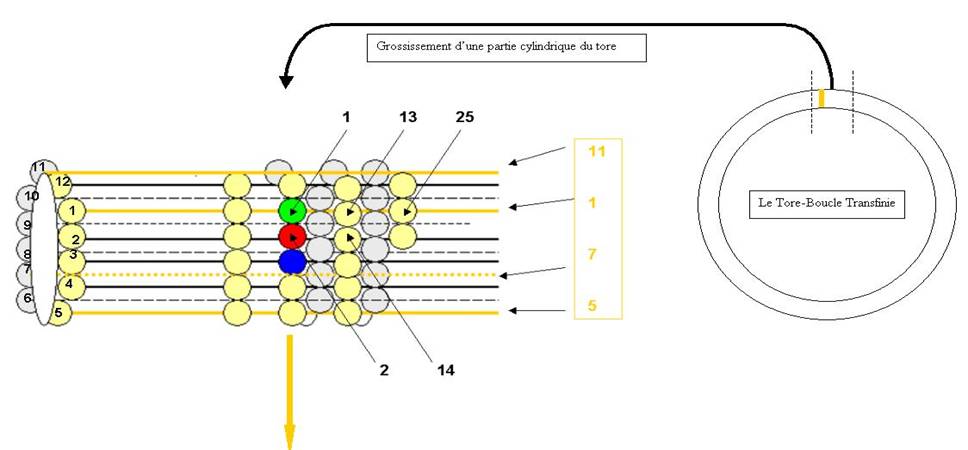
J’ai représenté ci-dessus la partie du tore qui porte « le début » de la suite des Nombres : 1,2, 3, 4 , 5…….. 20, 21, 22, 23,24,25…enroulée en hélice…
Avant… se trouve l’Origine !
La suite des
Nombres se déroule dans les 2 sens, à partir de l’Origine
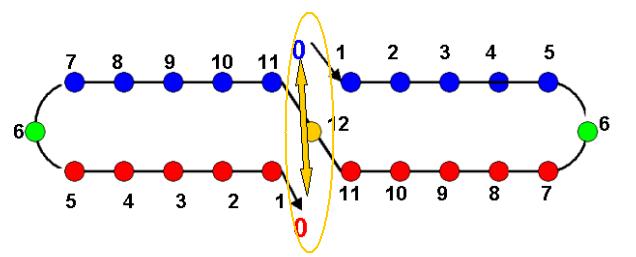
Voici la première spire de 1 à 12…je la considère comme superposition de 2 spires en sens inverse :
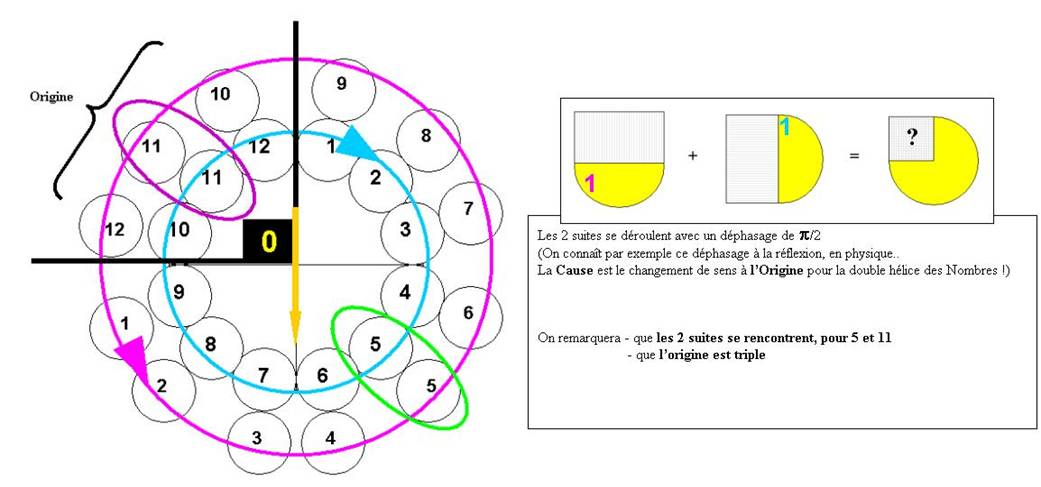
Il y aura en 5, un échange, que je représente ci-dessous, dans les 2 sens :
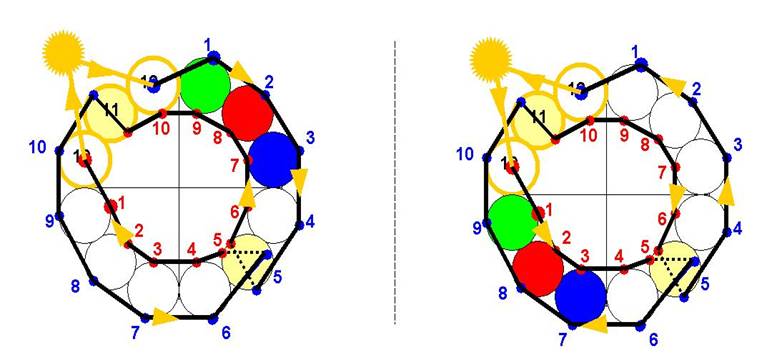
11 assure le lien entre les 2 extrêmes de l’Origine, qui se rejoignent d’autre part en reliant le début et la fin : TWIST
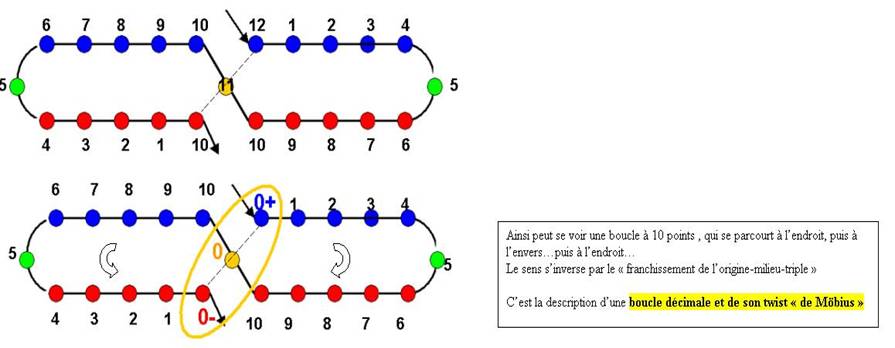
![]()
![]()
Etude du Twist :
( je ne représenterai qu’un sens dans la suite) :
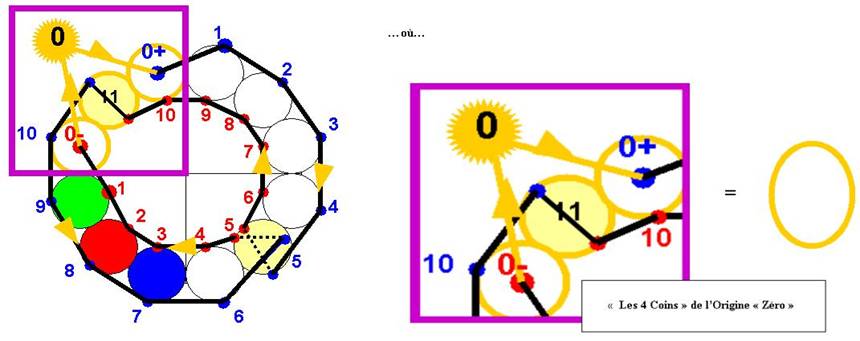
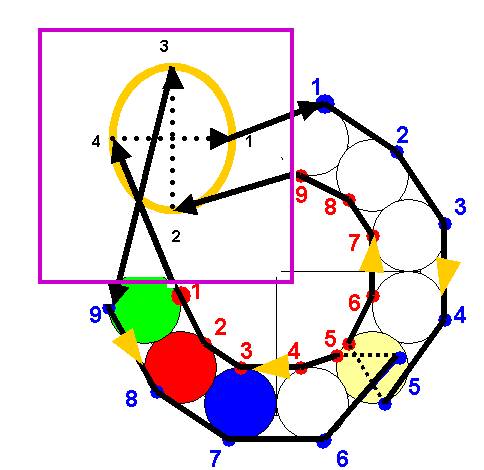
Dans le double parcours de la Boucle 12, qui est le parcours endroit-envers de la boucle décimale, il y aura 4 étapes dans l’Origine Zéro…
L’étape 1 est le début au point 0+…
La
cinquième ferme le circuit, c’est le retour
de 4 à 1 début qui devient
aussi la fin
L’0rigine, appelée « zéro » présente pour chacun des 2 sens, 4 valeurs :
(j’explique ci-dessous ce schéma)
« Les quatre coins » sont occupés par les valeurs 0 et 10 (unité décimale 1)
0 et 1 sont atteints dans le sens croissant et le sens décroissant que j’ai notés + et -
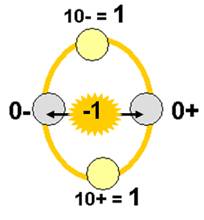
Les 2 valeurs de 0 se rejoignent en un point que je pourrais appeler (-1)
Les 2 valeurs de l’Unité 1 se rejoignent en 11 , que je peux voir comme = (leur égalité)
La double nature du 0 décroissant et croissant, change notre façon de compter !
On introduit une origine – 1 !
Le système décimal est un anneau de Möbius twisté !
n a maintenant le choix… (ou l’obligation !)… de compter avec les 2 sens des Nombres !
Il y aura deux origines 1 et –1, qui représentent simplement deux sens de parcours…
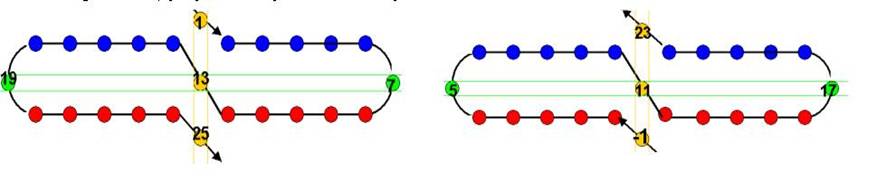
Il y aura alors deux hélices en sens inverse…
On remarquera que - dans la somme-superposition des 2 hélices, chaque point est égal à la somme des points milieu
ici 1 + 23 = 19 + 5 = 13 + 11 = 17 + 7 = 25 –1 = 24 et 24 = 2 x 12 avec 12 = (13 + 11) /2 (12 est la moyenne des 2 milieux)
- dans chaque hélice la somme des points des médianes diamétralement opposés est égale au double point milieu
Exemple : ici 1
+ 25 = 19 + 7 = 26 = 2 x 13 et 23
–1 = 5 + 17 = 2 x 11
La position de superposition des 2 hélices est la représentation d’une boucle de Möbius… à 12 points !
Le système duodécimal, dont l’unité est une boucle de Möbius à 12 points définit la structure des nombres et le système décimal.
Pour se faire une idée de l’enroulement de l’hélice à double sens qui est « multiple du ruban de Möbius » voici quelques exemples :
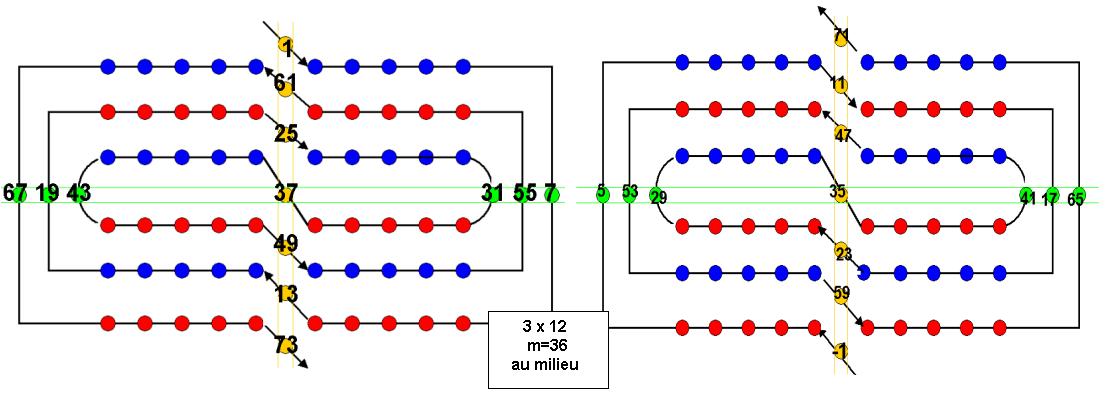
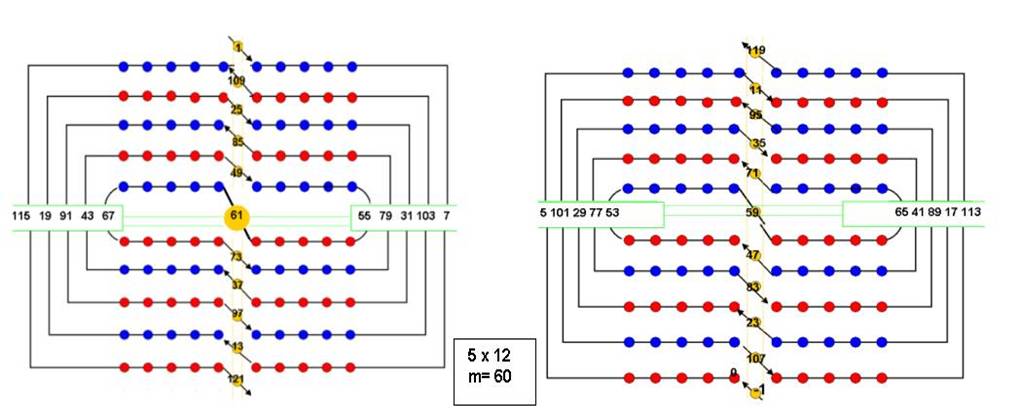
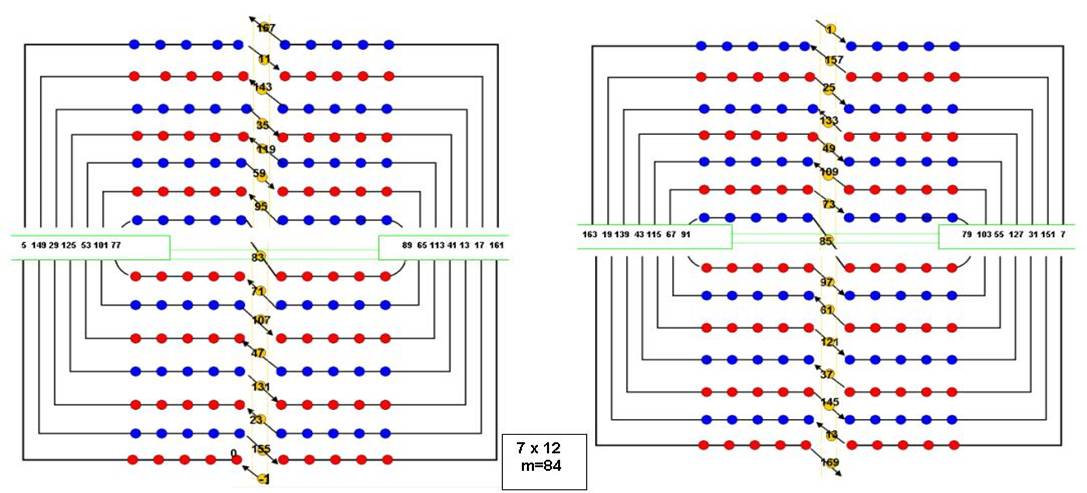
On vérifie que :
- En superposant les 2 enroulements , on trouve dans chaque cas la même valeur du point… égale au double milieu = 2 m (si m est le milieu, multiple de12)
Exemple ci-dessus : m= 84 pour 7 spires 5 + 163 = 149 + 19= …71 + 97… =168= 2x 84
- La somme de 2 valeurs diamétralement opposée est toujours la même, dans chaque enroulement (2m1 =166, 2m2=170), avec m = (m1 + m2)/2
Les 2 enroulements représentés ci-dessus sont endroit et envers d’une boucle de Möbius qui formerait m spires sur le Tore Transfini…
La Boucle de Möbius qui pourrait recouvrir le Tore Transfini , y formerait N spires… N étant le transfini
N serait alors milieu… et aurait un double…
Le Transfini a un
double …
Le Transfini est une Paire…
Si le Transfini est l’Infini UN… UN + UN = UN