Avant les
nombres… la quantité
Les nombres
n’existeraient pas encore au début de ce chapitre.
Mais la quantité existe et peut
être mesurée, ou « comptée »
Nous allons
considerer dans ce chapitre des petites quantités ou « quanta » carrées,
toutes identiques.
(si je cherche
un nom pour les appeler « quanta, carré,carreau,
quatre… quarra ou carra… kara »
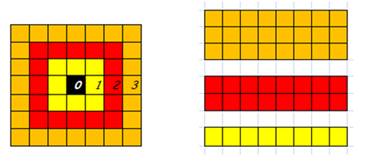
Soit un karum initial,
représenté comme un
petit carré noir, il peut être parfaitement entouré par « huit* »
autres de même nature.

Ce seront « les 8 premiers » que j’ai
rencontrés au cours de mes chapitres sous différentes formes, et que
j’ai nommés ainsi.
*huit : Le nombre 8 est ici
génant, je veux me placer dans le cas où les nombres
n’existent pas encore : il est difficile d’en faire totalement
abstraction, tant les nombres sont inscrits dans notre quotidien.
J’écrirai
au besoin en
italique ces nombres (non existants ici encore) , mais qui sont ceux
que nous utilisons habituellement.
Un tour
supplémentaire (ici en rouge) est formé par une quantité
double ( 16 carrés entourent les 8 précédents
jaunes)
Le tour suivant
(en orange) contient une quantité triple ( 24 kara = 3x8 kara)
Si on
considère les « 8 premiers » comme unité de quantité , et le
karum initial comme origine « 0 »,on définit les
nombres 0,1,2,3.
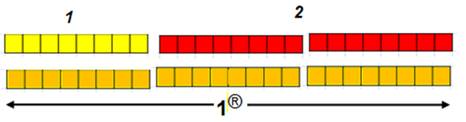
On a aussi la
relation entre nombres que nous connaissons 1+2 = 3.
Je choisis cette
quantité comme unité :
24 kara = 1®
Remarque :
le nom de l’unité rencontre
une double cohérence : nous connaissons « l’or 24 carats » !
. ® est le symbole
que j’ai introduit dès le début de mon travail pour
représenter « la
réciprocité », elle se révèle
déjà dans ce chapitre.)
Elle est telle
que 3 = 1®
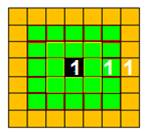
Le carré
représenté ci-dessus peut apparaitre alors comme un contenant avec son contenu.
Contenant et contenu ont la
même valeur 1® , quand on considère le quantum initial comme origine « 0 » vide, et
l’unité ci-dessus définie
Ce carré peut alors être défini
soit par son contenant (orange) ou par son
contenu (vert) : valeur NOMBRE.
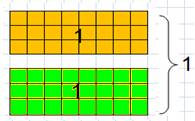
Cette définition numérique sera le NOM du
carré, qui pourra être porté par le vide, au milieu, que
l’on appellera « Juste Milieu ».
Ce Nom assure le
lien entre contenant et contenu, et constitue l’unité du
carré, que l’on nomme ici : « UN = 1 »
Le Juste Milieu représente le carré dans
sa complétude, qui est telle que 1 = 1 +
1
Le NOM du carré ci-dessus crée le NOMBRE 1 , avec une
forme CARREE.
Il est construit
sur la relation 1=1+1
Cette relation
qui nous semble paradoxale (puisque nous l’écririons
1 = 2 ) , est telle que
1 = 1 + 1
avec 1 = 1 =
1.
Nous avons écrit aussi ci-dessus :
3 = 1® , que nous écrirons 3 =1
Apparait alors
la relation particulière des 3 nombres 1,2,3 qui peut paradoxalement
s’écrire 1 = 2 = 3 quand on considère le
nombre dans sa complétude
contenu-contenant.
Ce lien particulier de réciprocité sera une première
justification de l’exception
que je fais dans le chapitre suivant pour les nombres premiers.