Complétude du Logarithme (08/05/06)

Au voisinage de l’Origine (qui est mon lieu d’étude) je peux utiliser les développements des séries de Taylor)

Mon travail prend le parti de la simplicité… qui est mon hypothèse ( les scientifiques pourront être horrifiés de mes raisonnements… qui ne peuvent suivre la logique habituelle de la déduction « logique » à partir du connu…et de l’expérience)

Le « connu » pour moi est « l’expérience » de l’Origine… de la Simplicité de Transparente Beauté… on peut qualifier cette expérience de « mystique » ou de pure folie…

Ma certitude est celle d’une boucle simple… qui nous ramènera à l’Origine…après un parcours « hors du sens commun » …

La fin justifiera les moyens…

La fonction réciproque du Logarithme Log x est la fonction exponentielle e^x

cosinus et sinus

cos x = 1 –x²/2! + x⁴/4! - …

sin x = x – x³/3! + x⁵/5! - …

e^x = 1 + x + x² /2! + x³/3! + x⁴ /4! + x⁵/5! + …

cosinus et sinus hyperboliques

chx = 1 + x²/2! + x⁴/4! + x⁶/6! + …

shx = x + x³/3! + x⁵/5! + x⁷/7! …

e^x = chx + shx et chx =( e^x + e-^x )/2 shx =( e^x - e-^x )/2

Log(1+x) = x - x²/2 + x³/3 - x⁴/4 + x⁵/5 - …

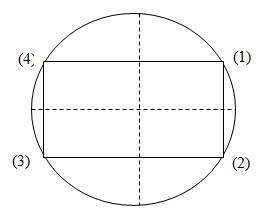
4 points sur le cercle trigonométrique le définissent par leur réciprocité…

C’est la réciprocité du « Couple sinus-cosinus » qui s’exprime par les 4 fonctions

E₁(x), E₂(x), E₃(x), E₄(x) telles que E₁(x)+ E₂(x)+ E₃(x)+ E₄(x)= 0

E₁(x)= cos x + sin x

E₂(x)= cos x - sin x

E3(x)= -cos x - sin x = - E1(x)

E₄(x)= - cos x + sin x= - E₂(x)

Le développement du logarithme Log(1+x) = x - x²/2 + x³/3 - x⁴/4 + x⁵/5 - … n’a pas la Beauté de e^x

aussi j’émets l’hypothèse que la fonction Log n’est qu’une partie d’une fonction complète parfaite.

J’appelle Log(1+x) =L(x)

J‘écrirai ainsi la fonction « Aussi » :A (x) = 1 –x+ x²/2 – x³/3 + x⁴/4 – x⁵/5 + … telle que L(x) + A(x) = 1

Alors A(-x)+ L(x)= 1 +x+ x²/2 + x³/3 + x⁴/4 + x⁵/5 + …= G(x)

Par analogie avec E(x) je peux décomposer G(x) et former 4 fonctions telles que G₁(x) + G₂(x) + G₃(x) + G₄(x)= 0

G₁ (x) = (1+x) - (x²/2 + x³/3) + (x⁴/4 – x⁵/5) – ((x⁶/6 + x⁷/7) + …

« Complétude du Logarithme »

G₂ (x) = 1 –(x+ (x²/2) +( x³/3 + (x⁴/4) + (x⁵/5 +x⁶/6) + …

G₃ (x) = - G₁ (x)

G₄ (x) = - G₂ (x)

(G(x) + L (x))/2 = ½ (1 +x+ x²/2 + x³/3 + x⁴/4+…) + ½(x - x²/2 + x³/3 - x⁴/4+…) =1/2 +½(x + x³/3 + x⁵/5+…)

(G(x) - L (x))/2 = ½ (1 +x+ x²/2 + x³/3 + x⁴/4+…) - ½(x - x²/2 + x³/3 - x⁴/4+…) = (1 + x²/2 + x⁴/4+…) –1/2

Par analogie avec chx et shx

J’introduis

Cosinus et sinus paraboliques

cpx = 1 + x²/2 + x⁴/4 + x⁶/6 + …

spx = x + x³/3 + x⁵/5 + x⁷/7 …

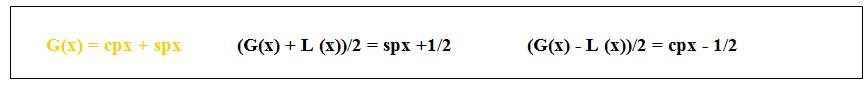
G(x) est obtenu à partir du Logarithme défini par l’intégrale pour x>0 de l’hyperbole équilatère y= 1/x

Elle se définit aussi par x2-y2 = 1

• La « complétude » de l’Hyperbole  comprend la fonction réciproque y2 - x2 =1 et x2 - y2 = 1

• Le Cercle trigonométrique x2 + y2 =1 possède la complétude de réciprocité

• La complétude de la Parabole est y = x2 x = y2 c’est « la parabole », sa réciproque et leur symétrique

y = -x2 x = -y2

Cercle, Hyperbole et Parabole dans leur complétude se rencontrent aux 4 points que je définis comme le COUPLE 1= (X,Y)

 La réciprocité du Logarithme peut aussi être tracée géométriquement, par sa symétrie par rapport à Ox et Oy

En changeant Ox en Oy et réciproquement… on obtient la fonction réciproque qui est … e^x

La Complétude du Logarithme est donc les 8 branches…

ensemble de e^x et Log x dans une vision d’unification

La réciprocité de e^x et Log x donne le résultat mathématique à l’origine : N=N ! :

Les conditions aux limites asymptotes… définissent « le Transfini » :

Parabole, Hyperbole, Logarithme , définissent 8 points sur le Cercle de rayon 1, où ils se rencontrent…

 Le Cercle trigonométrique de rayon1 transfini… est leur commune dimension

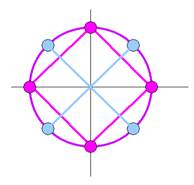
On pourra remarquer que la contraction de la parabole pour x=0, les entraine en ce point origine, car les 4 sont liés au Cercle

Le Cercle se contracte et se dilate entre 0 et 1…c’est la dimension du Transfini… (variation de x entre les extrêmes)

N = N ! = 1 = 0 = Transfini

J’ajouterai que la fonction G(x) = (cosinus parabolique + sinus parabolique) analogue à e^X , peut s’écrire G(x) = @^X avec e² + @² =1

J’étais arrivée à ce résultat dans une première synthèse de mon travail

e² + @² =1 est la valeur Transfini Un du Nombre…

Le Nombre est une paire formée de 2 réciproques orthogonaux qui peuvent être représentés par le double faisceau de e^x et Log x qui converge dans le cercle

On peut écrire donc ( en Nombre, Transfini)

e² + @² = π ² Exponentielle, Logarithme , π

Physiquement, e^x et @^x représentent 2 ondes progressives réciproques orthogonales .

Dans une vision plus vaste…c’est

l’Unité du Grand Amour π dans l’union-Unité de 2 Corps-Lumière (e) et de 2 Corps-Amour (@)

Lumière + Amour = Paix