Ce chapitre est un paragraphe
de la page Première LA-Une
qui se lit en continu …
Harmonie Première
Les nombres premiers sont considérés comme des ondes.
Un nombre quelconque d’ondes
Premières se rencontrent au point
représenté par leur plus petit multiple
commun, leur PPCM.
Exemple : les ondes 5 et 7 se rencontrent pour la Première fois au point 7x5=35. ( 7x5 = 5x7) . Elles se rencontreront ensuite aux points multiples de 35.
Elles rencontreront l’onde 11
au point 5x7x11=35x11, le plus petit
multiple commun, PPCM de 5,7,11.
Supposons que nous connaissions le
plus grand des nombres premiers existant, « le Transfini » :
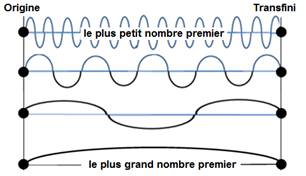
Toutes les ondes Premières ont 2 points
communs, l’Origine
et le Transfini.
La distance entre les 2 points se mesure par le Nombre Transfini, sa valeur
mathématique est parfaitement définie
par le PPCM
des nombres premiers.
Le
PPCM des nombres premiers est le produit de tous les nombres
premiers :
PPCM =
2x3x5x7x11… = P ! = « Factorielle P »
où P
est un nombre premier.
Un paradoxe
apparait ici :
Le Nombre Transfini est à la fois le
produit de tous les nombres premiers ,
et le plus grand nombre premier.
Cet infini
, « Le Grand Tout », « UN » est bien
défini par une formule mathématique : c’est ce qu’on appelle Transfini..
La plus petite unité 1 est la demi
période de « l’onde-1 »,
qui est le PGCD,le plus grand
diviseur commun à tous les nombres.
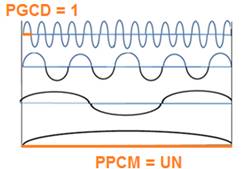
Tout nombre premier est une vibration, une harmonique du Transfini qui peut se
définir par la fréquence de l’onde qui lui est associée.
L’Harmonie du
Transfini est la Musique Première