Le Nombre dans la
réciprocité 4
La réciprocité 4 existe aussi dans la structure du nombre et dévoilera d’autres propriétés.
Les schémas ci-dessous expliquent cette structure qui donne en particulier une autre interprétation du ZERO
-
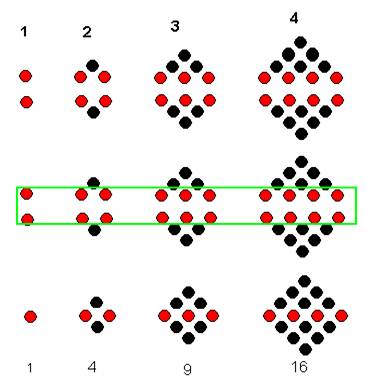
Les nombres 1,2,3,4…tels que je les avais définis dans « nature et représentation du nombre »
, sont vus dans leur réciprocité 4 : les
- Cette unité se fait par « collage » (ligne 2) tel que :

Ce lien ou collage exprime la condition de réciprocité 1 = 2 qui a été trouvée dans « construction d’une perfection »
- La ligne 3 représente le Nombre dans la
perfection du lien réciproque de ses 4 quarts :
( 1 3 6 10 15 21 28 …) x 4 +1 :
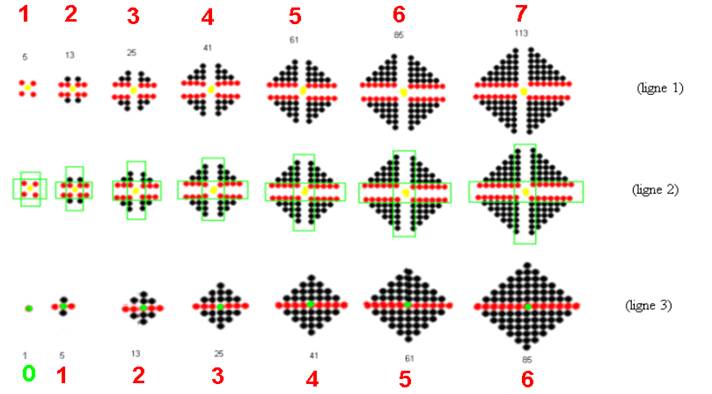
J’introduis la valeur « NOMBRE » (en rouge), en décalage avec la ligne 1 :
La cause du décalage est l’existence du ZERO, qui est ici point central Origine 0, c’est le point de Cohérence , de Cohésion des 4 quarts :
(1 3 6 10 15 20…) x 4 + 0
Le ZERO est le lien de
Cohérence qui construit l’Unité de Réciprocité 4
Ce lien établit une autre série (1, 5 , 13 , 25 , 41 , 61 , 85…) qui a des propriétés intéressantes :
· La série « lien »
Elle « fait correspondre » ou se déduit de la série 4N et la série des carrés, par un tableau d’addition :
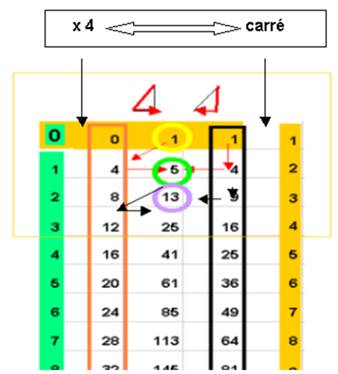
La série lien et la série carrée peuvent être représentée par des surfaces (carré et « carré losange »)
On pourrait voir entre les deux, un « twist perpendiculaire », ou en parler comme « 2 réciproques perpendiculaires » :
La structure de ces 2 carrés (5x5
dans mon exemple) est différente :
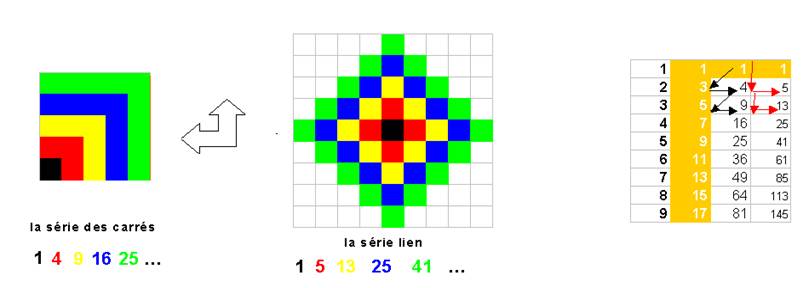
La structure du carré losange donne avec ses lignes celle de la série impaire (1,3,5,7…)
La série impaire construit, par le tableau d’addition, la série des carrés puis la série lien .
Elle construit l’identité 1+3+5+7+ …+ (2n-1) = n2
Ces constructions seront étudiées dans la structure des Pyramides apportant de nouveaux résultats
· La série carrée peut être construite aussi à partir des nombres définis par la série lien 1, 3, 6 10…
Mais ils seront représentés sous la forme «géométrique twistée » ! (le lien se fait par l’hypoténuse)
Ainsi , voici les 2 représentations du 4
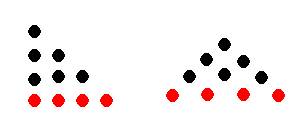
(1 3 6 10 15 20…) x 2 :
· Dans le chapitre « construction d’une perfection », on a vu que chaque nombre est aussi somme des précédents…
Ainsi dans la réciprocité 4, le nombre évolue vers sa complétude :
Voici des exemples :
….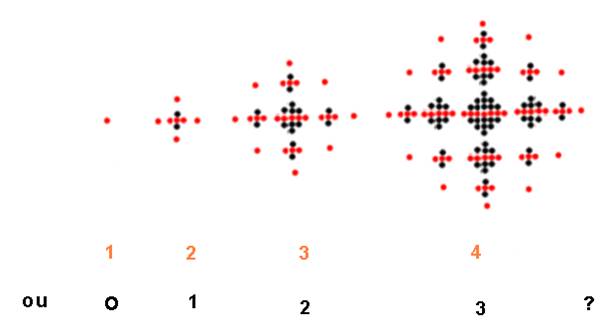 .
. 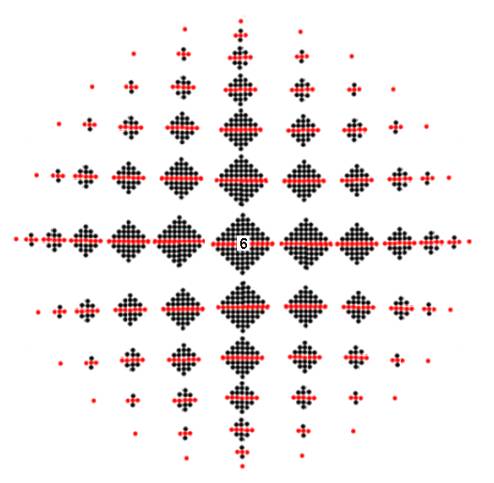
la construction du 6 continue…
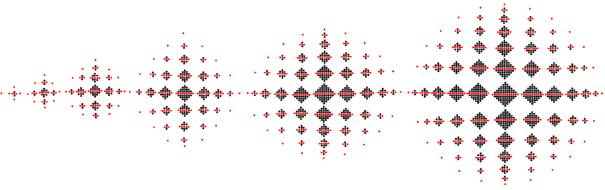
… vers sa complétude…

… dans sa réciprocité…

… et ce n’est qu’un commencement… un niveau à compléter…. dans une imbrication d’infini…
Le Nombre est ainsi contenu dans un Cercle, qui est Sphère dans nos 3 dimensions.
Il est tentant d’essayer de calculer son périmètre et son diamètre pour … en déduire une valeur de π … ?
Ce sera le sujet du chapitre suivant.