Construction d’une perfection
Dans ce chapitre , je complète l’étude du nombre défini
comme contenant et contenu
, pour décrire les bases de ce que j’appelle « réciprocité »
J’introduis « le tableau d’addition » et le
« tableau symétrique d’addition » qui permettront la parfaite symétrie réversible
A partir de la structure, définie dans le chapitre précédent, qui est en cohérence avec la suite de Fibonacci, on peut construire une autre définition du nombre plus complète :
Je représente ces 2 définitions dans le tableau ci-dessous :
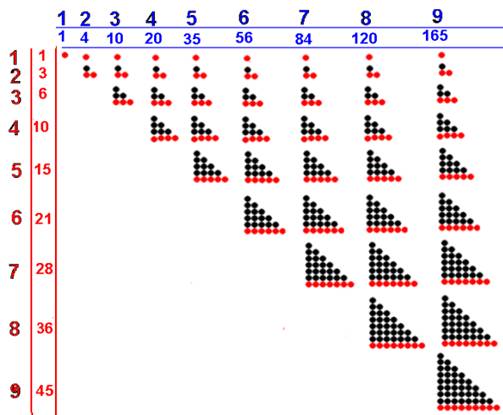
Le tableau, montre 2 niveaux dans la construction du nombre
- Première définition (la série des contenus est en rouge) c’est la construction vue dans le chapitre « nature et représentation du nombre »
1 est représenté par 1 point
1 = 1
2 = 1 + 2points = 3 points
3 = 2 + 3points = 3 + 3 = 6 points
4 = 3 + 4points = 6 + 4 = 10 points
….
- Deuxième définition (la série des contenus est en bleu), à partir de la première
Chaque nombre contient aussi tous les précédents :
1 = 1
2 = 1 + 2 = 1 + 3 = 4 ( les valeurs des nombres sont celles calculées par la première définition)
3 = 1 + 2 + 3 = 1 + 3 + 6 = 10
4 = 1 + 2 + 3 + 4 = 1 + 3 + 6+ 10 = 20
Ces valeurs s’expriment facilement par un tableau d’addition
La formule d’addition est copiée dans chaque case du tableau à 2 colonnes :
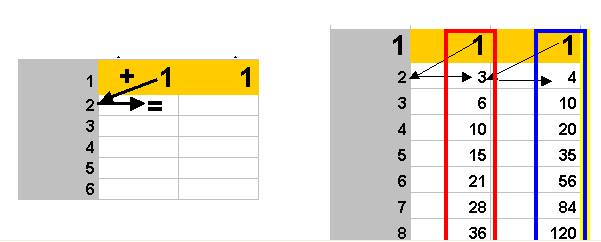
On y reconnaît le résultat de la première définition (rouge), et celui de la deuxième définition (bleu)
Utilisant le nombre dans ses 2 définitions, j’explique les étapes qui construisent la réciprocité :
-
Etape 1 :
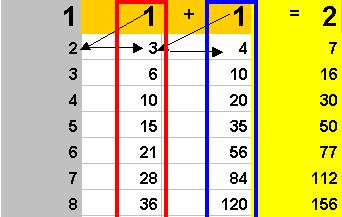
C’est l’addition
« classique » des 2 colonnes : 1 + 1 = 2
-
Etape 2 :
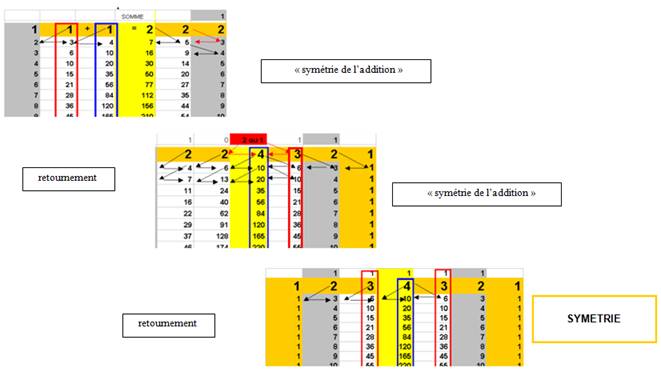
Il existe une « symétrie » qui reforme la suite des nombres entiers naturels (1,2,3,4…)avec un décalage (qui sera plus loin expliqué)
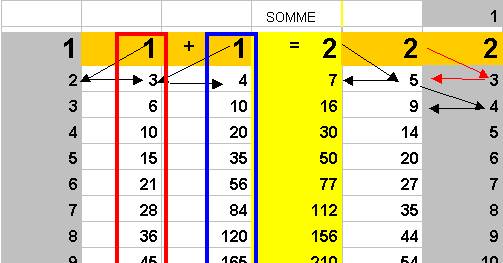
C’est le tableau symétrique d’addition ( en lisant le tableau ci-dessus, et le sens des flèches on retrouve ses additions)
Il n’est toutefois pas possible de le remplir automatiquement par cette règle d’addition, que l’on peut toutefois faire mentalement.
C’est ainsi qu’apparaissent
2 + 5 = 7 C’est ici 5 qui est calculé, comme
différence de 7 et 2… on calculera 7 – 2
, en introduisant l’opération de soustraction
On remarque que l’opération n’est pas symétrique
-
Etape 3
Il s’agit d’une
« symétrie » par retournement
On repart du résultat de l’Etape 2 , pour construire le tableau d’addition ci-dessous
On y inclut l’Etape 1 : la somme des colonnes donne ici 2 + 2 = 4
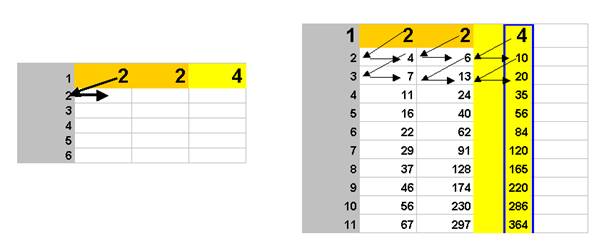
On constate 2 résultats intéressants
- le tableau d’addition ajoute les 2 premières colonnes dans la colonne jaune (ce qui n’était pas le cas à l’étape 1)
- la colonne somme est la colonne bleue (décalée d’un rang)
-
Etape 4
On complète la symétrie du tableau d’addition (comme à l’Etape 2)
On remarque qu’il est difficile d’écrire le 1 de la colonne jaune !
Il est 1 d’un coté et 2 de l’autre… Il est donc 1 ou 2 … la condition 1 = 2 résoudrait le problème :
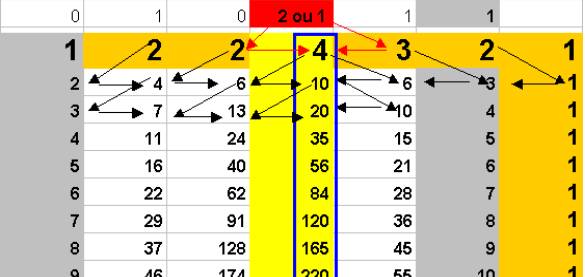
-
Etape 5
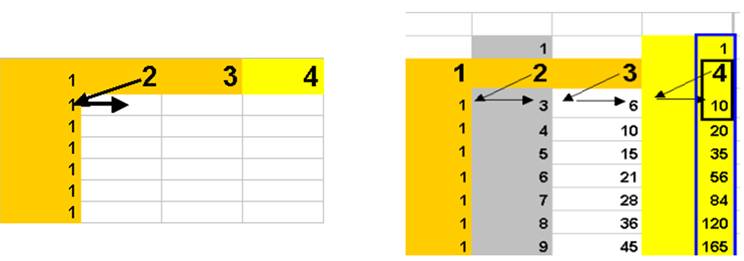
Comme à l’Etape 3, on fait un retournement
La colonne-somme se déduit du tableau
d’addition 1-2-3-4
·
Résumé : Construction de la réciprocité :
Les étapes de « réciprocité » qui construisent la parfaite symétrie , la réversibilité
Il semble évident en voyant ce dernier tableau que la
symétrie existe… Elle est pourtant dépendante de la condition 1 = 2
·
Propriété du 4
On peut noter que
- dans la « définition » bleue» du nombre 1 + 2 + 3 + 4 = 4
donc 4 = 10
- dans la « définition rouge » 4 = 10
Avec le décalage des colonnes, on peut lier 4 au nombre 1 de la suite initiale des entiers (chiffres or sur l’image suivante) , et ainsi est introduit aussi le ZERO :
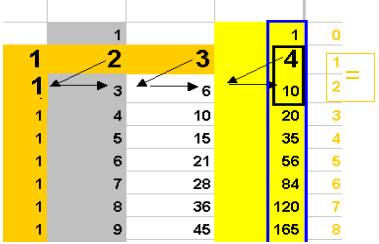
Cette correspondance
4 = 4 =10
et
4 = 1 forme
la première cohérence qui constituera
l’Unité décimale 1
= 10
Cette relation 4
= 1 est la base de la théorie de la
réciprocité : L’unité
est 4
Elle est aussi dépendante de la condition
1 = 2
Le décalage permet d’introduire le ZERO auquel est attribuée la valeur 1
Le Zéro est le Grand Contenant, vide…
Le nombre est somme contenant + contenu : ainsi
zéro est 1 contenant, avec 0 contenu = (1+
0)= 1
0 est 1 : c’est sa valeur de contenant
Le contenant est toujours 1 (point or)
Ci-dessous, la série (0,1,2,3,4…) des nombres définis par leur contenu et leur contenant :
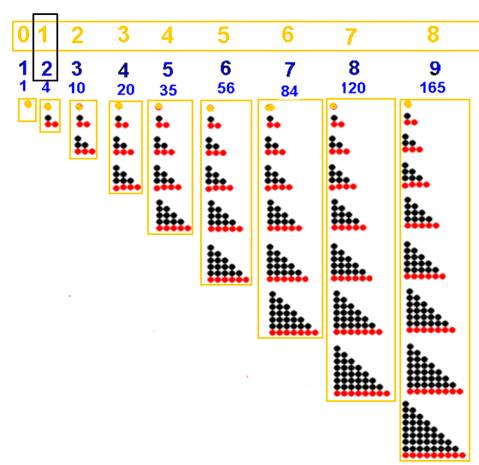
L’introduction du contenant ZERO est cause du
décalage, qui n’est autre que la condition 1 = 2 = (1 ou 2)
Cette condition est aussi 1 =
2 = 4
C’est la loi de la réciprocité 4, que j’ai aussi appelé « Loi 421 »
La position du 2, illustre cette loi : « chacun est double et moitié »
·
La cinquième colonne
Il faut inclure la 5ème colonne qui introduit le zéro, pour obtenir la symétrie de l’unité 4 = 1 + 2 + 3 + 4
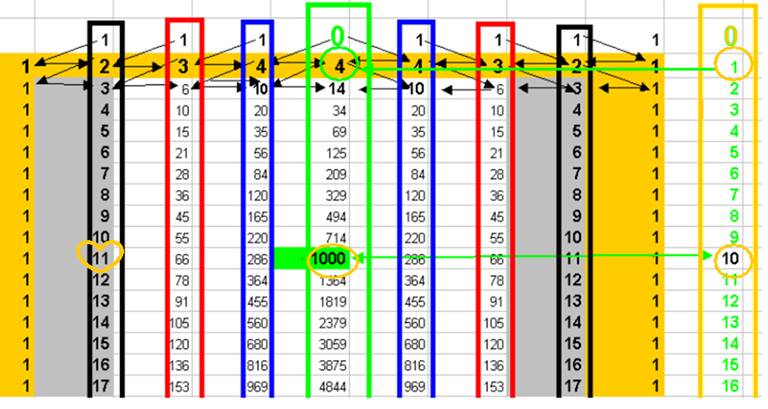
La cohérence décimale se confirme avec 1000 = 10
On remarquera que cette unité correspond au 11 de
« notre » suite initiale 1,2,3,4,5,6 ….
L’ unité 4 comme somme 4 = 1 + 2 + 3 + 4
est superposition des 3
définitions des nombres (noir, rouge, bleue étudiées précédemment) et du Grand
Contenant (orange) qui est l’Unité 1
(1,1,1,1,1…) : Le ZERO
(Ces séries se retrouveront comme base de la structure des empilements de sphères ou de cubes qui constituent les Pyramides )