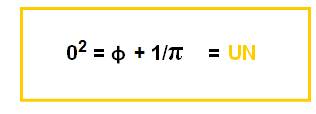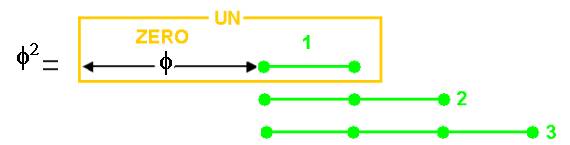
Dans mon travail j’ai montré que la suite des nombres
s’enroule , puis que le cercle existe
A l’origine cette propriété est déjà :
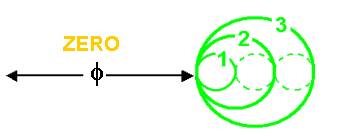
… et de là s’origine la valeur de π que nous
connaissons :
L'unité 1 s’enroule : π donne sa valeur au
diamètre de ce cercle : 1/π
La suite des nombres se construit :
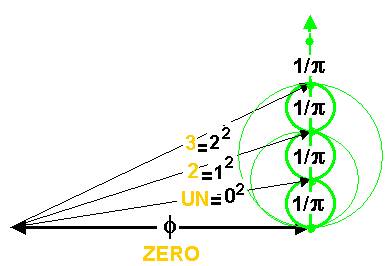
Les cercles ont respectivement les périmètres 1,
2, 3… , qui correspondent aux diamètres 1/π 2/π 3/π …
Si on considère la suite des nombres qui s’enroule en spirale, alors le nombre est représenté par la longueur de cette spirale de pas1/π :
1 =1
2 =1+2
= 3
3 =1+2+3 =
6
4 =1+2+3+4 =10…
Chacun des nombres contient les précédents ( c’est la série 1, 3, 6,10… qui se retrouvera dans les pyramides.)
- Nous avons découvert le sens du signe + :celui de 2 réciproques perpendiculaires.
(Ce qui nous amènera à la fameuse formule de Pythagore : au niveau protomathématique , elle se traduit par la simple addition).
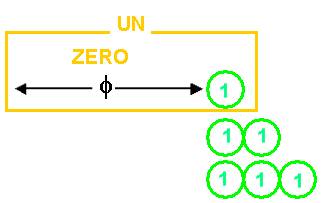
puis pour faire apparaître les triangles rectangles qui donnent sens au carré des nombres :
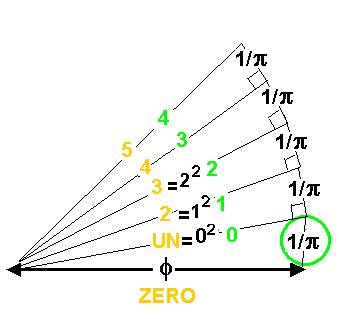
Le zéro entraîne un décalage : c’est celui de l’origine relative, qui donne son origine aux nombres que nous utilisons.
Nous utilisons ces nombres sans voir qu’ils sont en réalité des carrés
J’ai montré que le carré est le contenu du nombre .
L’utilisation que nous faisons de l’origine relative, peut être représentée ci-dessous :
Nous ne tenons pas compte de φ et prenons la valeur π = 1
Les
nombres sont alors utilisés dans leur « incomplétude racine » 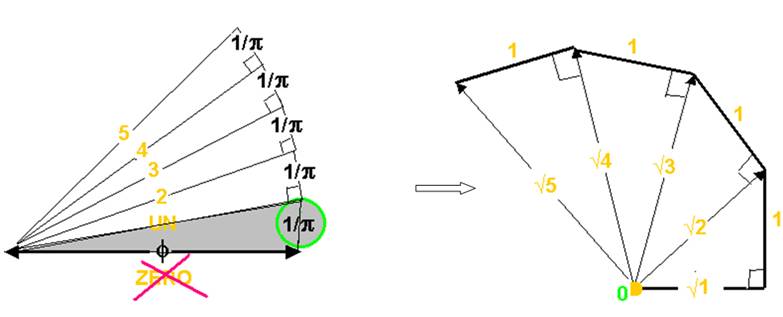
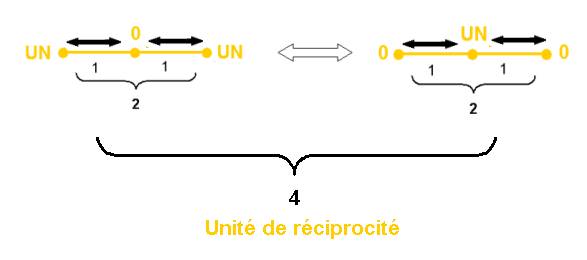
La spirale ainsi obtenu peut se construire dans sa forme de complétude symétrique, ou forme de « réciprocité 4 » :
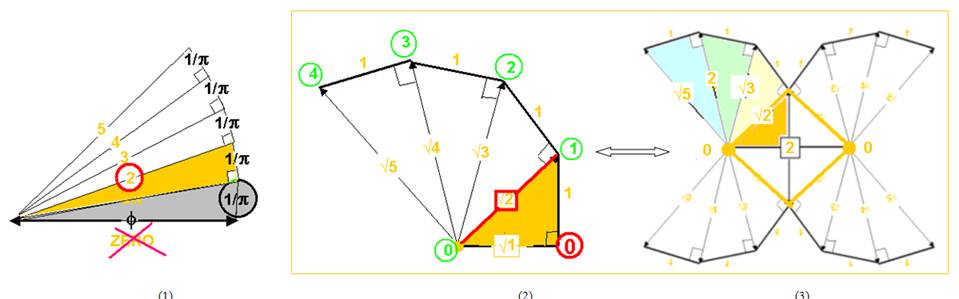
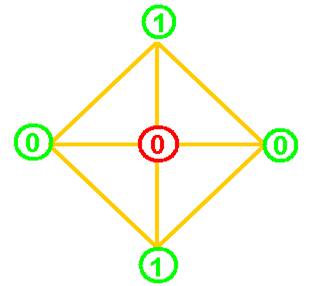
On peut considérer alors un ZERO
central, au centre d’un carré de coté V2
Avec ce centre, la série des nombres s’enroule dans une spirale « quantifiée » en segments de longueur 1.
Chacun des nombres correspond à la longueur de la spirale
depuis l’Origine Centre : 0
Le nombre est aussi exprimé comme le carré de la racine que définit avec un décalage le rayon vecteur :
Le décalage entre le nombre et la valeur du rayon vecteur est expliquée par la présence des 2 zéros, dont tient compte la série de Fibonacci. :.ici 0 et 0
On pourra noter « le raccourci » que donne le zéro relatif : la distance entre 0 et 1 est alors V2, ou même son carré 2, quand on n’oublie pas le Nombre d’Or φ et π
(shéma 1 ci-dessus). On peut alors écrire l’égalité 1 = 2
Le Carré central, origine de la
réciprocité spirale est
Dans le lien réciproque de 4 spirales est illustrée la dissociation paradoxale de la double origine dans la relation de réciprocité perpendiculaire :
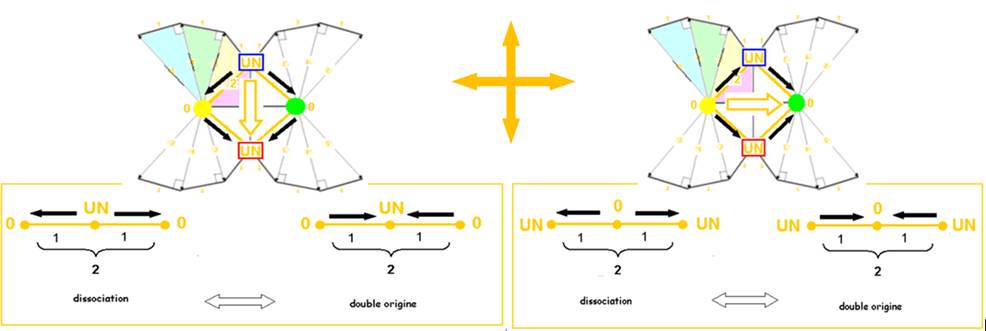
Elle peut être représentée dans la simplicité du symbole réversible :
Remarque :
C’est la construction de ces triangles rectangles qui a été ma première étude mathématique !… et qui m’a
permis de construire « la
belle fleur d’Or » :
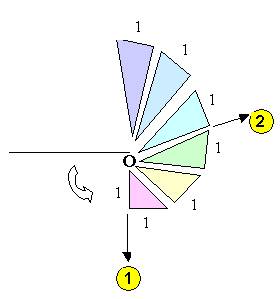
On remarque entre 1 et 2( valeur du rayon vecteur) , que la distance est 3 sur la spirale :
La distance entre 1 et 2 , est 1
On retombe sur la condition 1 = 3 qui définit le « relatif absolu »
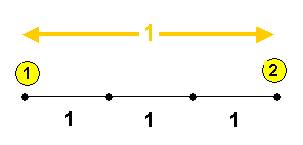
Si on ferme la boucle … les tiers deviennent des quarts : c’était mon étrange première découverte : « les tiers élastiques ».
La réciprocité 4 est mise en évidence .( tous les 1 sont égaux).
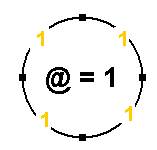
Elle s’exprimera de façon plus mathématique plus tard par la relation qui caractérisent la sphère et le cercle 2@ = 4/3
Je l’exprimerai aussi par 2@ π = 1 ou @ = 1
Ces simplifications peuvent être vues comme des abstractions mathématiques s’approchant de la perfection symbole de l’UN
Mathématique et « vision mystique » pourraient alors se rejoindre dans une belle Boucle Cercle .
Ces nombres de l’origine φ, @, π, G, k, i, e…donnent leurs propriétés aux nombres que nous utilisons tous les jours…
Les diverses séries qui ont été rencontrées dans ces chapitres, pour construire la perfection de réciprocité peuvent se déduire de la spirale en vision continue.
·
La spirale continue
Ce serait une spirale d’Archimède de pas 1/π
Cette spirale peut se construire dans les 2sens , par symétrie : (sur le schéma, elle est en rouge et en vert)
Les cercles de périmètre 1, 2, 3… représentent la série des nombres
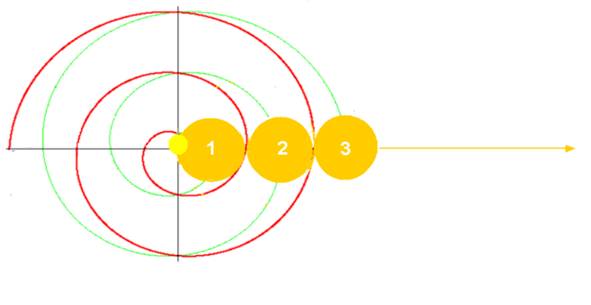
Pour tracer cette spirale, il suffit de porter « le cercle UN » sur un axe , ou cercle de diamètre 1/π = 1*( sur le schéma)
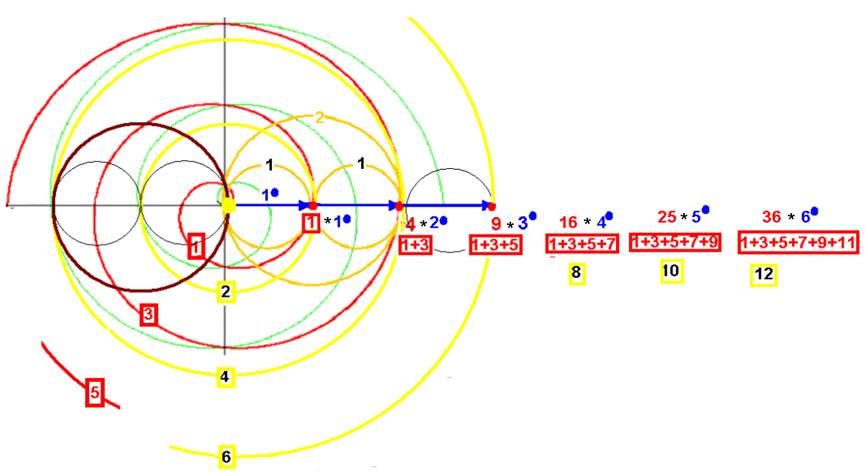
La spirale de pas 1/π définit les séries des carrés, paire, impaire :
Avec le pas de 1/p, la longueur des spires est 1,3,5, 7…(série impaire) , ce qui correspond à une longueur de spirale 1, 4, 9, 25, 36…(série carrée)
Les cercles circonscrits ont pour circonférence 2 4 6 8… (série paire)
2 est le nombre tel que 2x2= 22 4 est l’unité parfaite 4 = 4
Si le périmètre du cercle
est égal à son diamètre : le nombre π est alors 1 « transfini », les points de
l’axe peuvent s’écrire 1, 2, 3, 4,….,
Ces points apparaissent
avec leur carré (en rouge) , ils sont donc racine de cette valeur… on pourrait dire que 1*,2* ,3*…ou 1/π, 2/π ,3/π sont
les « racines –cercles » des
nombres 1,2,3,4…
Sur les points de l’axe, « la racine cercle »
donne une double définition des nombres : double( en jaune) et
carré (en rouge)
Nos nombres n’en sont que la moitié.
Chaque nombre se définit
par le cercle contenant de la spirale.
Voici une image de réciprocité 4 de cette spirale, qui peut apparaître comme « les 8 premiers »
On peut choisir vision
endroit-envers, contenu-contenant… :
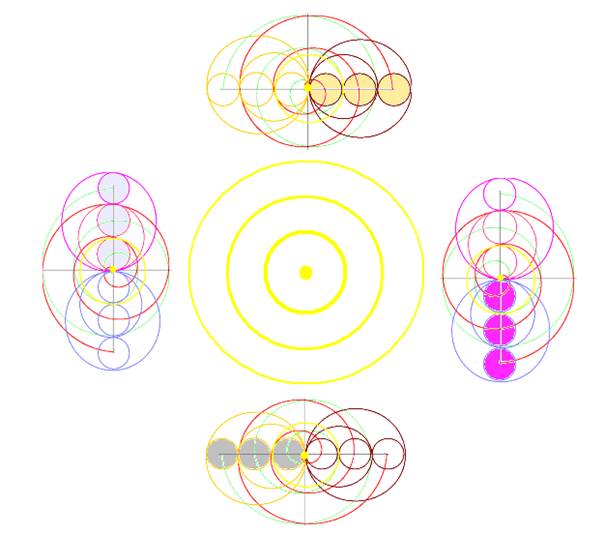
·
Quel est le lien de 2 spirales ?
Il est double :
-l’Origine ZERO
-le nombre N infini
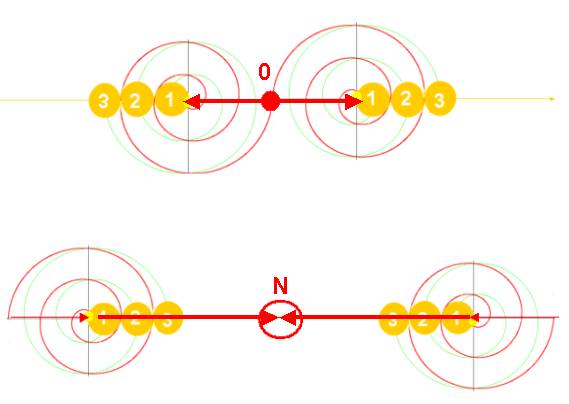
Mais, par la réciprocité ou réversibilité de la spirale…sa complétude dans les 2 sens …

… on peut se rendre compte que N = 0
C’est ce que l’on appelle le TRANSFINI ou UN =ZERO
C’est la vibration transfinie :