Etrangeté et nature de π

Le Cercle Transfini

Les nombres premiers , sont vus comme « ondes premières »

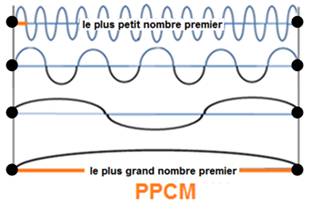
Les ondes premières se rencontrent au point représenté par leur plus petit multiple commun, leur PPCM.

Exemple : les ondes 5 et 7 se rencontrent pour la Première fois au point 7x5=35. ( 7x5 = 5x7) . Elles se rencontreront ensuite aux points multiples de 35.

Elles rencontreront l’onde 11 au point 5x7x11=35x11, leur plus petit multiple commun, PPCM de 5,7,11. Etc….

Le PPCM des nombres premiers est le produit de tous les nombres premiers :

PPCM = 2x3x5x7x11… = P! = « Factorielle P » où P est un nombre premier. 

PARADOXE :

Le plus grand nombre premier est aussi le produit de tous les nombres premiers en nombre infini.

Paradoxe d’un infini , qui est bien défini par une formule mathématique , on l’appellera «  Transfini ».

Cet « infini », le « grand Tout » , se définit : UN = P!

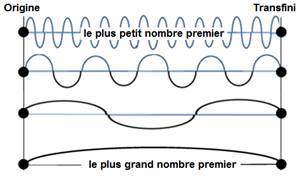
Toutes les ondes premières ont 2 points communs, l’Origine et le « Transfini ».

La distance entre les 2 points est parfaitement définie par le PPCM des nombres premiers.

Les 2 points extrêmes, Origine et Transfini , peuvent se rejoindre pour former une boucle fermée : … un cercle ?

Le seul cercle fermé ou «  Fini » serait le Cercle Transfini , fini par la rencontre paradoxale de 2 extrêmes opposés, l’Origine et le Transfini .

· Remarque :

Quand un cercle s’ouvre, apparaissent 2 extrémités

Ces 2 point extrêmes,ici l’Origine et le Transfini, correspondent à la disparition d’un point du cercle qui faisait leur lien, ou plutôt qui paradoxalement FERA leur lien .

Ce point qui existait et existera, EST, ABSOLU en tout point de la BOUCLE CERCLE, Cercle Transfini.

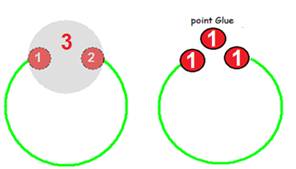
3=2+1 ou 1=1+1 .

C’est la vision ABSOLUE du TRANSFINI : UN = 1 = 3 =…. π (3,14…) 

π (3,14…) est la vision que nous pouvons avoir de cet ABSOLU

Paradoxe d’un « ABSOLU relatif » , dans notre vision limitée..

· Le « cercle π » est la vision paradoxale du Cercle Transfini :

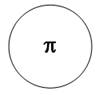
- son diamètre d est le UN Transfini

- son périmètre est le Nombre Transfini P! le périmètre d’un cercle étant π.d, ici le périmètre est π.UN= Π (valeur Transfinie de π)

Périmètre = P! = Π

Il faut voir Π dans la puissance de sa représentation numérique Π = 3,1416… 10^Π : c’est le nombre π que nous connaissons , imaginé sans la virgule.

PARADOXALEMENT

dans sa dimension Transfinie ( sans virgule) π = P! , le nombre π se définit comme :

- le plus grand des nombres premiers

- le produit de tous les nombres premiers

- le PPCM des nombres premiers :

-multiple commun à chacun des nombres premiers, il est divisible par chacun des nombres premiers .

… π LE PARADOXE des PREMIERS !

ACCUEIL