14 avril 2012
Dans l’étude des pyramides, j’ai découvert une suite intéressante qui fait le lien entre la série des carrés n2 des entiers et la série 4n.
Elle s’obtient par additions successives de 2 façons : - à partir de la suite impaire
-à partir de la suite des entiers n
Cette série fait penser à la surface du carré et
son périmètre.
On pourra remarquer toutefois, qu’il y a un décalage, si on considère la suite n des entiers de départ , et par suite l’existence d’un zéro.
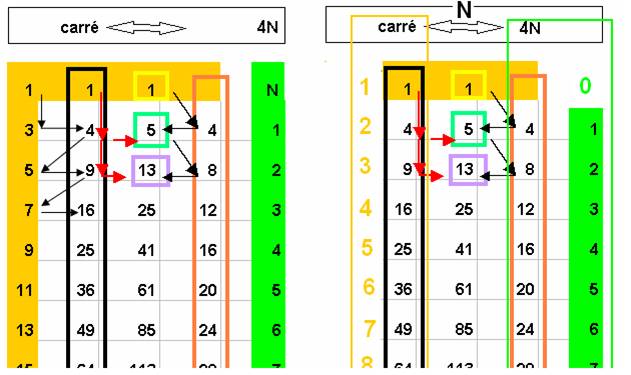
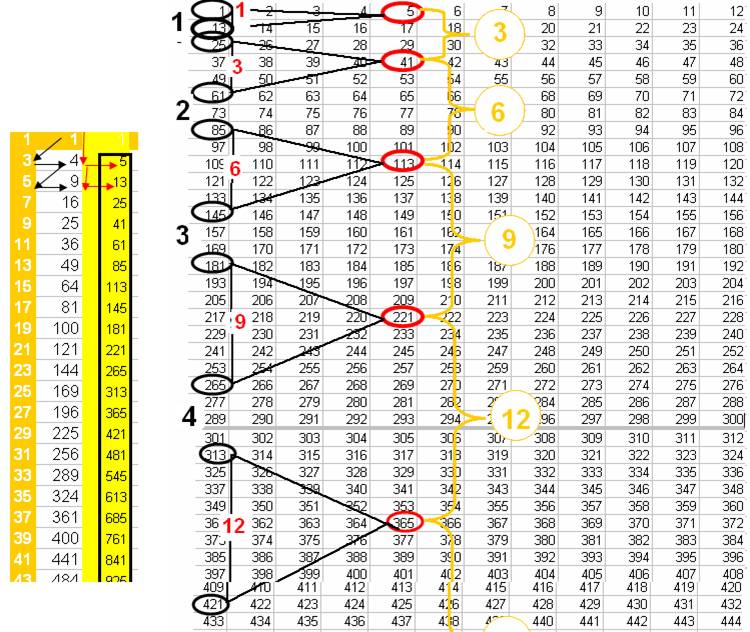
Quand les nombres s’enroulent sur la boucle-12 comme l’ont montré les nombres premiers , les nombres de la colonne lien apparaissent en colonne 5 et 1
J’ai noté sur le schéma ci-dessus les récurrences que j’observe.
La somme de 2 nombres (en noir) est la double somme du rouge +4 : exemple 181+265 = 2x221 + 4
1
+ 13 = 2x5 + 4
4 est le lien de la
paire. C’est le lien de réciprocité, qui fait son unité .
Je l’écris 4 =1 (si j’ai établi ce résultat , souvent déjà
a cours de mes chapitres, il sera encore justifié ci-dessous,
à partir de l’Origine).
Les 2 extrémités de chaque boucle ouverte, s’unissent dans le lien qu’elles forment : elles donnent la valeur somme à la boucle fermée, en son centre.
La première boucle est la boucle-12, quand 1 et 13 s’unissent .
Ce que je schématise ci-contre :
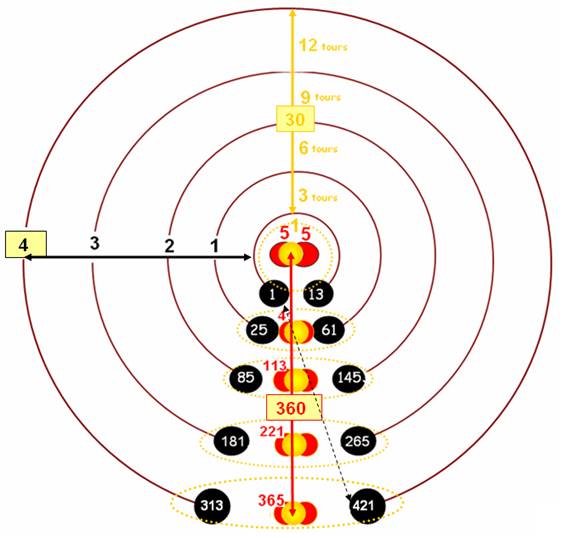
Remarque (« coïncidence »
ou cohérence qui m’amuse) :
421 ! c’est le début du 36ème tour (35 x 12 = 420) le lien avec l’Origine pour boucler la boucle en 1 ,« au 36ème dessous », le Juste Milieu.
Entre 5 et 365 la différence est 360
Il semble que 5 tours
sont « perdus »… ce sont les boucles (tracées sur le schéma ci-dessus
) contenants des tours dans chaque niveau que l’on peut voir d’une
façon plus imagée :
(J’ai représenté le couple de l’unité 5 ou l’unité du couple 5 comme « l’unité métaphysique », qui crée le lien de la boucle-12 initiale.
Notre lien avec les nombres n’est pas étrange… nous participons de la même Origine… c’est ce que montrera mon travail dans sa globalité. Certaines parties semblent encore difficilement soutenables pour un scientifique…)
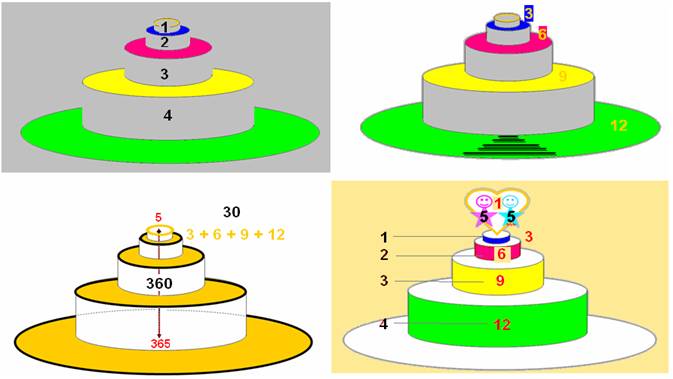
La série lien évoque
le carré…
Les liens représentés
ci-dessus, se retrouvent pour les carrés de coté respectivement 1, 4, 7, 10, 13 :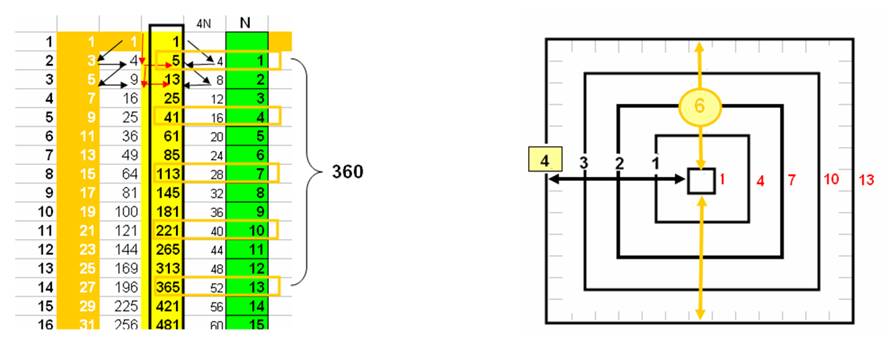
J’ai noté une analogie avec les cercles ci-dessus et j’ose une « superposition » :
La boucle-12 est
contenue dans le carré de coté1. La valeur contenue, le couple lié 5, est alors
l’unité 5 = 1 , qui permet l’égalité 30
= 6.
Le carré 4 contient parfaitement le cercle 4, mais les autres niveaux ne correspondent pas géométriquement : les écarts entre les carrés sont égaux et non entre les cercles.
Mais il existe un lien parfait entre carrés et cercles, dont j’explique ci-dessous la force :
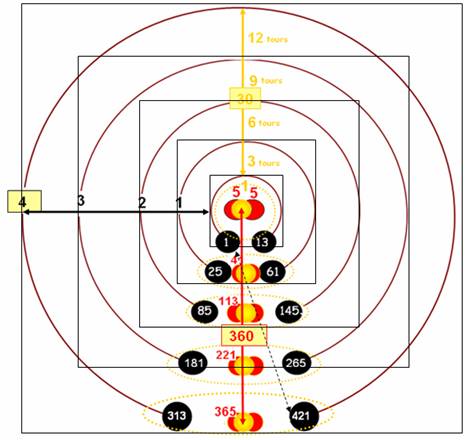 l
l
Les couches circulaires ont pour « contenant » la couche « disparue » qui fait leur lien .
12 tours sont contenus par un 13ème qui crée leur lien . Ce tour correspond au carré de coté 13.
9 + 1 =10 9 tours correspondent au carré de coté 10
6 +1 = 7 6 tours au carré de coté 7
3 +1 = 4 3 tours au carré de coté 4
1 + 1 = 1 le premier tour est contenu dans le carré de coté 1, ce qui donne l’égalité 1 + 1 = 1
La couche lien est donc « transformée » en carré ;
La géométrie du carré
suggère une symétrie d’ordre 4.
Lors de l’étude des nombres premiers j’ai vu que les boucles fermées ( multiples de 12) pouvaient être représentées par la réciprocité de 4 boucles. (Le lien avec la forme carrée semble donc cause de la réciprocité 4)
Nous avons trouvé ci-dessus un lien 4 entre les 2 éléments du couple.
C’est le lien de réciprocité, ainsi construit entre cercle et carré, qui ferme les boucles.
Ce lien est un mouvement d’échange et de partage , force toujours en mouvement qui crée toutes les mutations et « décalages » qui font la magie des nombres qui se développera encore dans le chapitre suivant.
![]() Voici une vision , imagée, de ce mouvement :
Voici une vision , imagée, de ce mouvement :
Le Grand Contenant Cercle-360 dans la réciprocité carrée en
mouvement
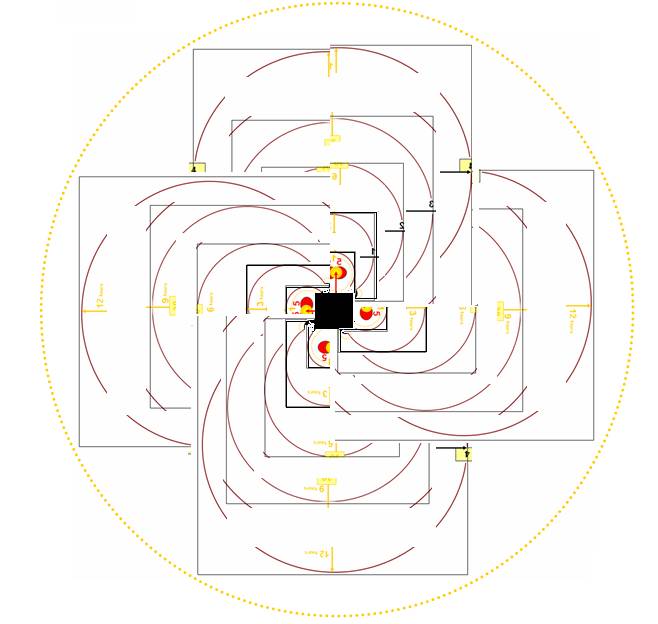
Ceci est une autre représentation imagée de la force du lien supersymétrique
*remarque :
(J’avais découvert la position particulière des nombres de la série lien par une réflexion sur les nombres impairs.)
Compte tenu du zéro les nombres impairs s’expriment sous 2 formes 2n-1 ou 2n +1 .
La surface entre 2 carrés est un nombre impair et la somme des impairs couvre la surface d’un carré, ce qui pourra s’exprimer de 2 façons :
(exemple représenté pour le carré de coté 5)
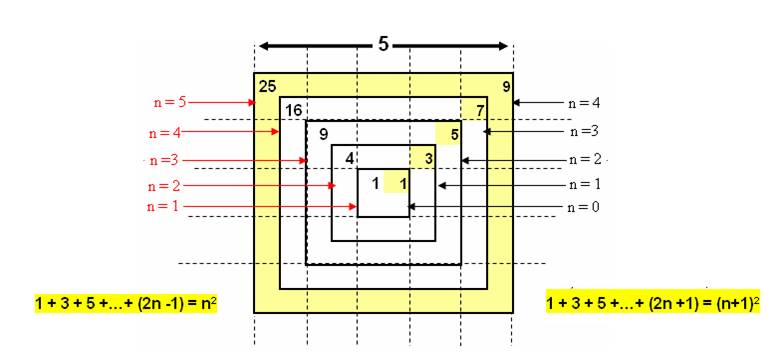
J’avais aussi montré à partir de cette série lien que par dissociations successives ![]()
Ceci permet de calculer la série paire, de 2 façons :
-en doublant la série ci-dessus : (2 + 4+ 6 + … + 2n) = n(n+1)
-par
différence entre la série entière et la série impaire : (2
+ 4+ 6 + … + 2n) = n(n+1)/2 – (n+1)2 =
(n+1)(n/2- n -1)=-(n+1)( n/2+1)
ou (2 + 4+ 6 + … + 2n) = n(n+1)/2 – n2 =
n/2
Ces résultats semblent étranges… si on les considèrent pour un nombre n fini.
L’égalité des 2
méthodes donnent les conditions :
n(n+1)
)=(n+1)(- n/2-1) n
=-( n/2+1) n = -2/3 et n
=-1
n(n+1)
)= n/2 n + 1
= 1/2 n = -1/2 et
n = 0
Elles s’appliquent à un nombre n infini ou transfini, c'est-à-dire pour le « Grand Tout UN » n=1 .
Ce nombre est représenté par la complétude-cercle, et sur ce cercle représenté par la boucle-12.
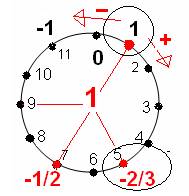
Je revoyais ainsi les positions particulières que je retrouve souvent au cours de mon travail (1,5,7,11) , que j’ai appelé « la réciprocité nombre-premier ».
Les nombres de la série lien apparaissent dans les colonnes 1 et 5, sur le développement de l’enroulement des nombres sur la boucle12 .