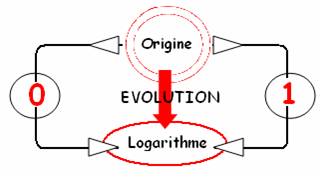
4 opérations et réciprocité
Opposés et inverses.
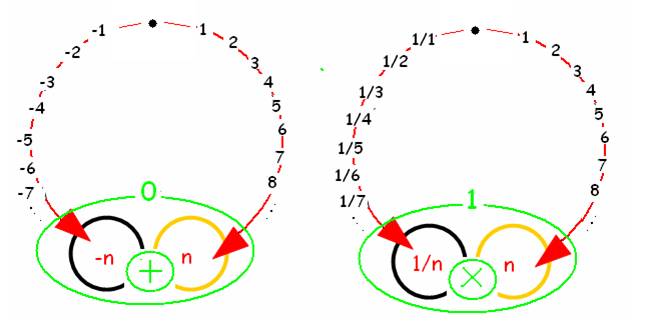
· A chacun des nombres de la suite des entiers que nous utilisons tous les jours (« positifs » : 1 , 2, 3, 4 , 5…n ) , peut être associée un « opposé : -n » , de la suite des entiers « négatifs » : -1,
-2, -3, -4….-n.
La somme de 2 « opposés » est égale à 0 : n + (-n) = 0.
De façon analogue on associe à chacun des entiers n son « inverse : 1/n », alors le produit de 2 « inverses » est égal à 1 : n x (1/n) = 1
· En regardant « dans l’autre sens », on pourrait dire aussi de façon « réciproque » :
- que 0 se dissocie en 2 opposés
- que 1 se dissocie en 2 inverses….
Chacun des 2 « retours » à l’origine qui se dissocie, forme alors une double boucle :
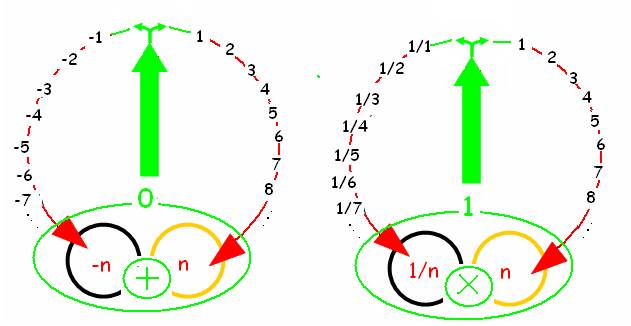
Le schéma suivant montre que :
L’origine des nombres, par cette « rétroaction » semble paradoxalement prendre deux valeurs : 0 et 1 :
0 est origine de 2 branches qui se rejoignent dans l’addition
1 est origine de 2 branches qui se rejoignent dans la multiplication
Addition et multiplication
pourront alors être considérées comme 2 « réciproques »
issus de la dissociation paradoxale en 0 et 1 d’une
Origine Unique
La fonction mathématique logarithme utilise et représente ce lien de réciprocité entre l’addition et la multiplication.
Je l’ajoute sur le schéma pour compléter une boucle qui
décrit « la complétude de la
dissociation paradoxale de l’Origine. »
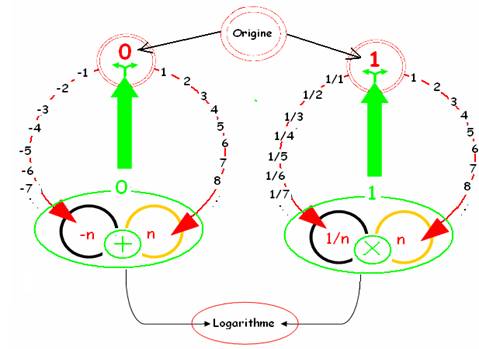
Le logarithme dont nous ne connaissons pas encore la complétude, ferme cette boucle, en liant multiplication et addition .
Ce lien que traduit, pour notre connaissance actuelle, la réciprocité de l’addition et de la multiplication, lie ainsi les 4 signes des opérations que nous utilisons : addition, soustraction, multiplication, division.
Le chapitre suivant étudie cette dissociation paradoxale de l’Origine, qui peut se voir comme un pas de l’évolution :
,