Echange et Partage : le ZERO
Les nombres φ et @ ont été étudiés au chapitre précédent
Nous connaissons la relation arithmétique « équation ». Elle peut être transformée par le passage d’un coté à l’autre de chacun des termes avec un changement de signe.
En pratiquant cette technique mathématique, nous ne lui donnons généralement pas de signification.
En considérant les exemples ci-dessous qui concernent φ nombre d'Or et @ l’alliance
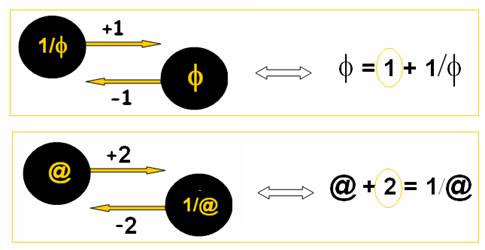
on peut dire
- que 1 s’échange entre φ et son inverse (ou réciproque)
- que 2 s’échange entre @ et son inverse
Cet échange se fait dans les 2 sens .
L’écriture de l’équation choisit et privilégie un sens, mais les 2 existent, à la fois.
Ainsi le terme « échangé » est mis en commun , partagé. Il constitue la relation, le lien entre les 2 réciproques.
Si on « ajoute » ce double mouvement d’échange, on pourrait « quantifier » cette relation et l’appeler « zéro » en lui ôtant toute sa valeur de partage.
Dans le circuit ci-dessous, j’ai utilisé ces échanges et la propriété de dissociation paradoxale pour établir la correspondance de « réciprocité » entre 2 niveaux « symétriques » par rapport à une origine :
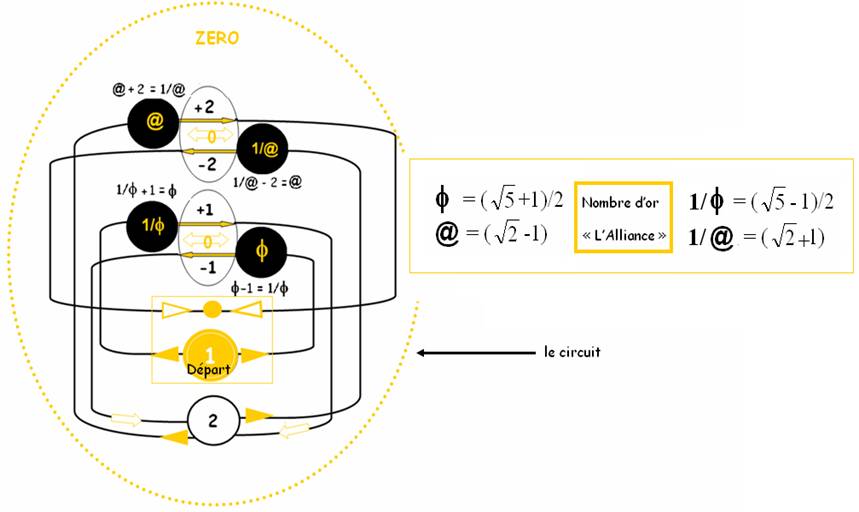
L’origine pourrait s’appeler 4, car elle « reçoit » 2 dans les 2 sens.
Cette somme est aussi 0 si on considère les 2 sens opposés (+2-2=0) , et l’origine « zéro » va ensuite transmettre cette valeur de partage, pour réaliser une harmonie dans toute la boucle…
Ainsi il y a mouvement dans les 2 sens dans le circuit , mouvement d’échange et partage qui crée l’égalité
![]()
(L’égalité 1 = 2 = 4 est ce que j’appelle « la
Loi 421 » de la « théorie de la Réciprocité »)
On remarquera que « zéro » est à la fois « le juste milieu », et le lien qui crée l’unité globale . Ce lien est la propriété du « Grand Contenant » que j’ai symbolisé par le pointillé.
L’ensemble est ce que nous appelons « ZERO ».
C’est une seule
« EQUATION » : le terme prend ici tout son sens d’
« égalité ».
C’est une seule
Unité .
L’ EQUATION ici serait donc :
« ZERO » = UN
Les chiffres que nous utilisons vont participer de ce même échange-partage .
Nous le découvrons dans le chapitre suivant.