Mai
2020 : je repousse une M.AJ de 2012 au bas de la page…
Je relève dans les premières lignes : « 2 visions
mathématique et protomathématique sont utilisées en même temps ! » …
d’où toute la difficulté à saisir ces
tableaux, expliqués par la suite... un génial glissement du chiffre au
Transfini !!!…qui traduit la « respiration » du grand Contenant !
Les Chiffres
La construction par enroulement décrite dans le chapitre précédent permet de donner des réciproques aux chiffres que nous utilisons .
Dans le tableau ci-dessous sont représentées les réciproques des « 8 premiers » ( dans tout mon travail précédent j’ai souvent rencontré « 8 premiers »).
Je leur ai donné des valeurs par analogie avec les deux premiers niveaux construits précédemment.
Les symboles de leur nom ne sont pas choisis au hasard, j’expliquerai plus bas les choix présentés.
Je représente la paire et son échange réciproque par un symbole unique
La paire formée entre 2 inverses établit un échange réciproque analogue à l’échange étudié dans le chapitre précédent.
Il y a toutefois un paradoxe qui se lève si on considère les nombres (que j’ai écrits en rouge) comme complétude 1.
Ici, les 2 visions
mathématique et protomathématique sont utilisées en même temps !
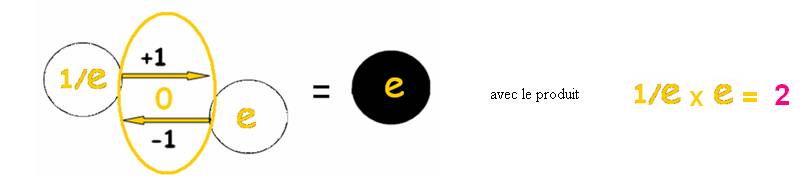
Les chiffres en rouge, se trouve ainsi simplifiés, dans la deuxième écriture du tableau :

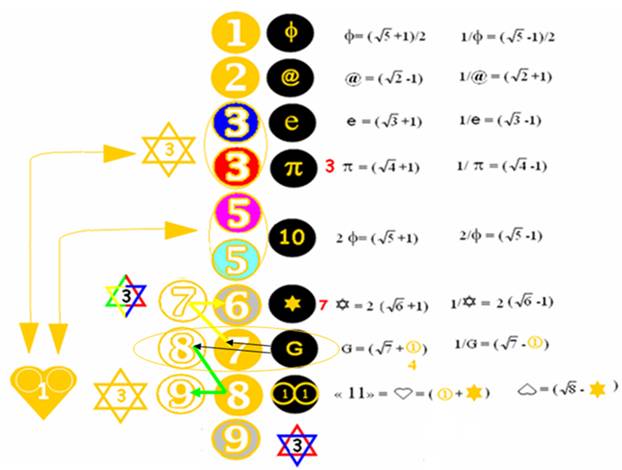
Je note dans le tableau ci-dessous les « justifications » de ces choix et leurs conséquences, je rajouterai ensuite des éclaircissements en commentant le tableau.

e et p sont des « nombres transcendants » qui ont des valeurs connues et établies, que j’ai encadrées en vert
G est une constante de la physique.
Des valeurs « approchées » de ces constantes et de 7, (entourées) sont données par le calcul avec les racines carrées..
(7 dans sa « réciprocité 4 » constitue la forme étoile du symbole réciproque du 6)
La valeur approchée de G est donnée en utilisant comme unité la valeur 4 : unité de réciprocité
Si on considère 1/G, on notera que si on utilise le nombre dans sa complétude carrée (au lieu de la racine), 1/G = 7-1 = 6, d’où G=1/6 et dans sa complétude de réciprocité 4 : G = 2/3
Le symbole du 8 , est représenté comme un huit perpendiculaire :11, deux unités jumelles ( ici somme de 7 et 4)
La valeur des 2 inverses encadre le 11
Des unités jumelles se rencontrent en 2 points du tableau :
3
= 4
5 qui se présente comme 2φ est double , ce qui crée l’unité décimale 10 et qui prend la place du 6, qui ainsi « disparaît ».
A la suite du deuxième 5 vient donc le 7 et il se produit un décalage.
Le 6 devient 7 ( on remarque que c’est la valeur approchée calculée et le symbole réciproque du 7)
Le 7 devient 8
Le 8 devient 9 : tous les chiffres apparaissent donc avec « les 8 premiers » et même le 10.
L’unité décimale ce construit avec les 4 premiers, qui sont unis de façon à ce que 1+2+3+4=10 =1 : les 4 sont l’unité décimale 4 = 1 : cela construit la loi de la « théorie de la réciprocité », dont mon travail est le sujet.
Cette réciprocité est construite par le lien entre eux , qui se traduit par 3 égalités qui définissent de 3 façons le nombre @.
Ces 3 conditions ont été déduites de la « théorie de la réciprocité » dont la seule hypothèse est l’existence d’une boucle fermée.
J’ai découvert le nombre @ comme condition pour que le cercle « se ferme » : la nature in-finie de la surface p du cercle de rayon 1, prouve que la définition de sa surface est… « incomplète ».
L’existence du cercle qui est pour nous une évidence, implique le lien des 4 constantes : (φ, @, e, π ) ou leur réciprocité
Les 3 valeurs de @, sont proches et « approchées »… une « malléabilité » qui rend possible toute l’évolution… et crée des nombres étranges, transcendants, beaux dans leur « irrationalité »…, et des constantes qui se font dépasser…
(Dans le tableau ci-dessus @ serait 2… qui est aussi 1 et 3, si on utilise 2 au lieu de sa racine)
Dans le chapitre précédent, cette « malléabilité » a été vue comme une harmonisation par échange et partage.
Mais il y a encore à dire… reprenons le tableau…évolutif :
G qui correspond à la fois à 7 et 8 se dissocie en 6 et 9, ce qui peut s’interpréter :
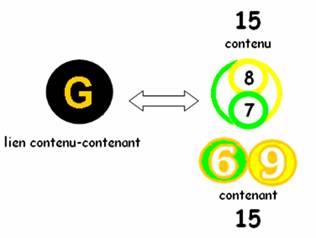
Sur le schéma enlacés apparaissent en couleur 6 et 9 qui sont contenants de 8 et 7.
La somme 8+7
= 6+9
G est alors lien entre contenu et contenant.
De la même façon sont liés 1,2 et 3 :

3 + 5 = 8 3 x 5
= 15
On remarquera le lien des nombres 3 et 5 :
- chacun est double
- leur somme 8 se montre dans le tableau ci-dessus
- G , par la réciprocité contenant-contenu construit leur produit :
Alors 3 est l’unité triple 1
15 est l’unité triple 5
L’unité décimale est la double unité 5.
Le lien contenu-contenant est un Grand Contenant qui donne les propriétés aux nombres, qui lie les unités.
Les mutations qui transforment les nombres de l’un en l’autre traduisent un mouvement qui crée le lien.
On peut le représenter par le double sens :
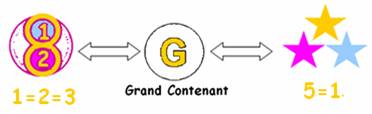
Pour traduire le mouvement , je ferai apparaître les signes (+1 et -1) qu’expliquent la « dissociation paradoxale »
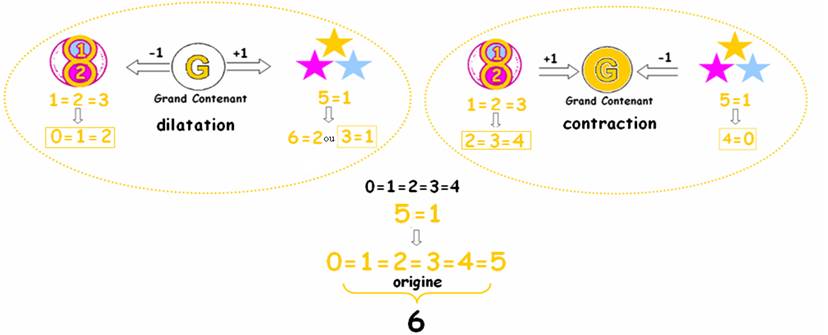
Ainsi le Grand Contenant se dilate et se contracte en donnant aux nombres leurs 2 valeurs extrêmes et voisines :
1 oscille entre 0 et 2
2 oscille entre 1
et 3, 3 entre 2 et 4 et… plus étrangement
5
entre 3
et 4 !
Comment ?
Il se forme 2 couples réciproques perpendiculaires :
Ils sont issus de la dissociation paradoxale de l’unité 1 de
réciprocité 4 en unité décimale et unité 6 ou ( dans l’autre sens) , sont vus comme créant cette unité :

Le
Grand Contenant oscille entre son centre et son extrême de
dilatation.
De façon réciproque, on aurait pu dire, dans l’autre sens, que c’est l’oscillation des nombres entre leurs deux valeurs voisines (celles de leurs voisins) qui produit celle de leur contenant.
On voit se former ce nombre 6, qui avait «disparu » en tant que contenant, il est formé de 6 contenants égaux : 0,1,2,3,4,5 :
Voici leurs contenus
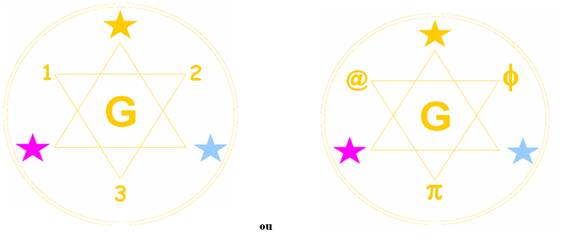
On est passé de
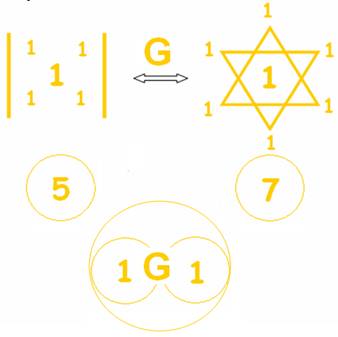
(mai 2020) Ci-dessous une M.AJ de 2012, qui me parait bien compliquée pour une aide à la compréhension… si claire quand je l’ai ajoutée… c’est le génie de la Pure Mathématique Origine !
M.A.J ; décembre 2012
Remarque :
Pour aider à la compréhension de ce
chapitre lire « la révélation du Nombre d’Or »
On voit
mieux alors le lien avec les nombres « étranges » :
constantes ou transcendants
Il n’est pas utile, alors, de comprendre
tout le chapitre pour passer à la suite'.
Le paradoxe protomathématique-mathématique peut être ici une difficulté .
J’ajoute un schéma exemple :
Sur cette représentation toute mathématique, peut être décrite la COMPLETUDE de l’origine ZERO , dans une vision de parfaite symétrie dans l’échange
partage des réciproques qui constituent l’ALLIANCE @.
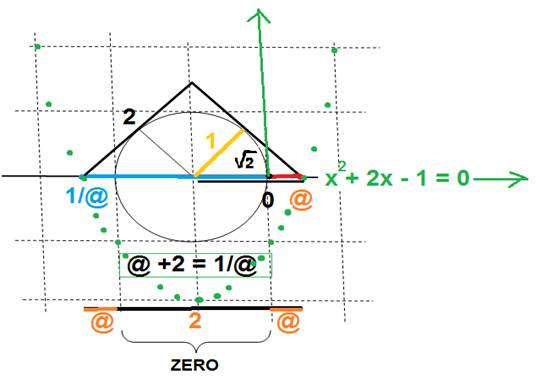
Je ne développe pas ici l’étude
mathématique (simple) qui permet de voir l’incomplétude de notre origine mathématique, qui se présente sous forme de dissymétrie pour nous..