… du Continu au Quantifié
…
… et réciproquement
J’ai observé que la présence des nombres premiers permettait de décomposer la suite continue des nombres, en ensembles ou « réciprocités » de 4 courbes fermées.
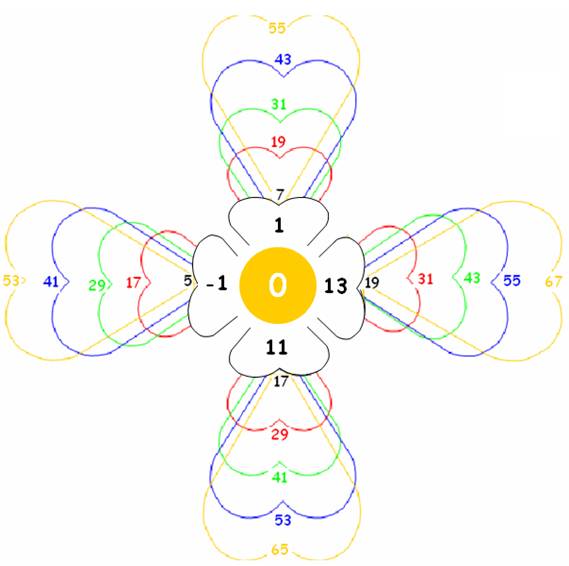
Dans le chapitre précédent, j’ai montré que le lien de 4 boucles 12 , est l’origine commune à chacun de ces ensembles de 4 enroulements.
Il apparaît comme l’origine 0 de chacune des courbes liées en ce point qui apparaît sous la forme (-1,1,11,13).
Le schéma ci-dessous (et le développement de son centre), résumé des observations du chapitre des nombres premiers, représente chacune de ces courbes, à son niveau d’enroulement :
(Pour une meilleure compréhension, je l’expliquerai au-dessous à partir de l’un de ses niveaux)
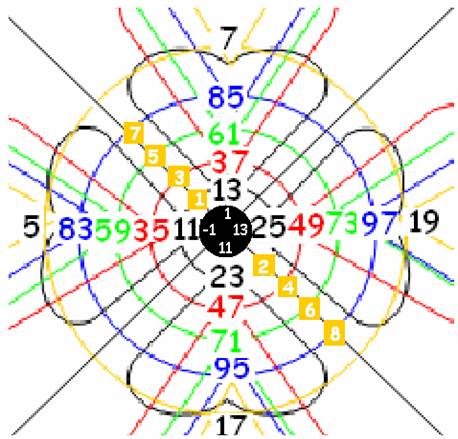
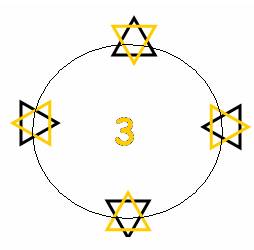
Ci-dessous le niveau représenté en rouge :
Les 4 courbes y culminent en 17,19,31,29.
Les origines liées respectivement à -1,1,11,13 sont : 35,37,47,49 que l’on retrouve sur le schéma du centre ci-dessus.
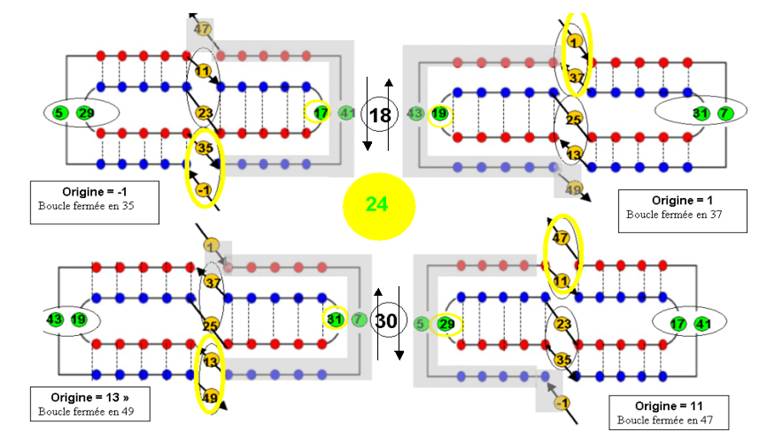
On remarquera que 17 et 19 se font face : ils sont liés par la présence manquante du 18 .
J’avais noté une double flèche : elle représente le sens de circulation dans les 2 courbes : le mouvement est le lien.
Ce lien par 2 mouvements opposés peut être appelé « Spin », c’est aussi ce que j’ai appelé « Twist »
De la même façon : 29 et 31 sont liés par un spin ou twist qui est la présence manquante du 30
A ce niveau, la longueur de chacune de ces 4 courbes est 36 (3 x12) , et serait (4 x12) sans le lien qui les unit.
Sur le schéma du centre, en rouge, apparaît sur des cercles concentriques l’enroulement de la suite des nombres : 3 et 4 figurent les passages respectifs de 35 à 37 et de 47 à 49.
Un saut se produit chaque fois que l’on franchit un multiple de 12 : la suite des nombres est enroulée en spirale sur un tore, chaque tour est une spire 12…
Le passage de la boucle fermée à la spirale est cause du saut.
La succession de ces sauts constitue la suite 1,2,3,4,5,6,7……
qui est construite sur un manque. (On
peut aussi la considérer comme le nombre de tours ou de spires)
Cette suite
« manquante » est dissociée en suite paire et
impaire.
- Etude de cette suite 0 1 2 3 4 5 6 7 …..
Tous les nombres
premiers et les multiples de 5, 7,11, sont voisins des « manquants »
, multiples de 6 et 12
(on les voit sur le schéma récapitulatif ci-dessous ou dans le tableau initial )
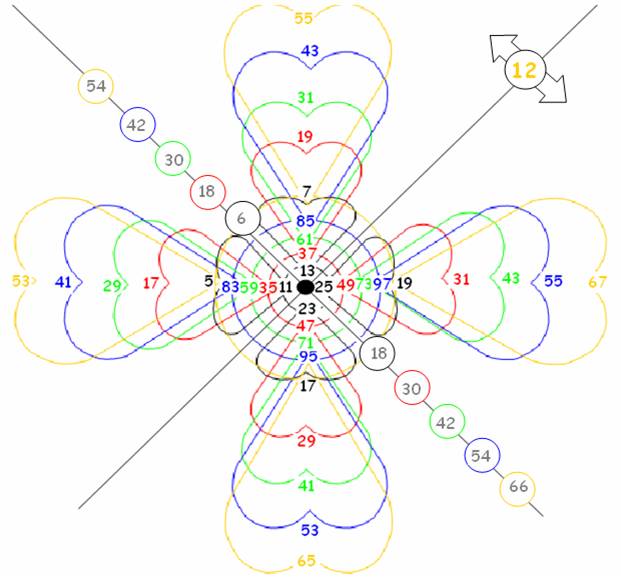
Ils témoignent de la construction de la suite des nombres sur une base 12… et de la pertinence du système décimal puisque sur 12 points… deux sont manquants !
- Observation :
L’absence des multiples de 6 dans la suite continue des nombres, va construire une nouvelle suite quantifiée : les unités de longueur 5 successives sont séparées.
Ces 2 suites sont représentées dans le schéma ci-dessous.

Une troisième suite, montre chacun des manques comme sa dissociation paradoxale : elle crée les « points premiers » : nombres premiers ou multiples de 5,7 11, qui l’encadrent.
Ceci constitue un lien entre de nouvelles unités de longueur 3. Cette suite est liée grâce aux « points premiers »
On peut voir alors cette ligne comme la suite continue d’unités paires de longueur 6.
Chaque paire est constituée de 2 moitiés « réciproques ».
On notera que cette nouvelle suite continue commence par un zéro qui est lui-même une
paire de réciproques .
- Sur la 2ème
ligne, l’unité 5 :

4 unités forment sa complétude : c’est un résultat de la théorie de la réciprocité qui nécessite la présence d’une boucle fermée .
La boucle se forme ou se ferme par « collage- disparition » des 2 extrémités grisées, qui sont apparues à l’ouverture de la boucle : (dissociation paradoxale d’un point qui n’existe pas)
Je schématise cette réciprocité « discontinue » ou « quantifiée » avec les « manques » qui font une boucle « ouverte » :

- Avec la 3ème ligne , on peut fermer une boucle continue, avec 4 unités paires 6, par le « collage » des 2 zéros.

C’est la réciprocité de l’unité 6 , ou double 3.
La boucle est représentée fermée.
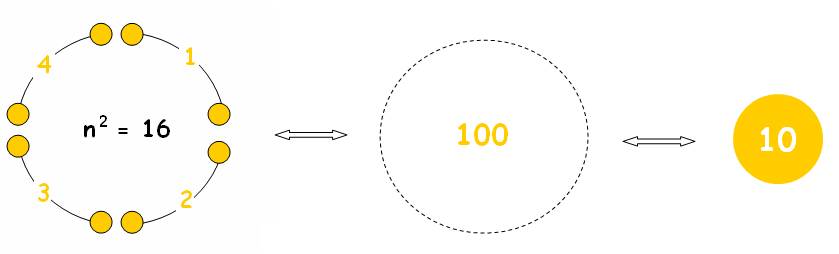
- La 1ère ligne a été utilisée jusqu’au point 25 ( carré donc complétude du nombre 5)
Si on multiplie par 4,
- on arrive à 100 (complétude de l’unité décimale).
- on pourra former 4 boucles 3 et 5 . C’est la complétude des boucles 3 et 5
Au niveau de la suite des paires liées , cette multiplication par 4 donne 16 unités et 8 zéros…
Ces 8 zéros seraient « les 8 premiers » .
Pour la théorie de la réciprocité : 16 = 42, est la complétude de l’unité 4 de réciprocité.
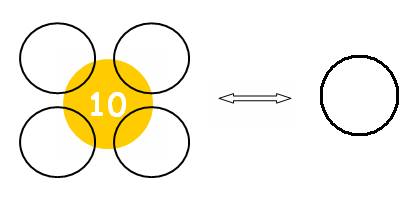
Les 8 zéros apparaissent, comme 8 extrémités quand la boucle se dissocie pour former la réciprocité 4 :
La complétude de l’unité 4 de
réciprocité est l’unité décimale.
Les 8 extrémités disparaissent pour fermer 4 boucles
réciproques liées par l’unité décimale.
L’unité décimale est le lien de 4
boucles, elle établit la complétude- boucle
(Remarque : les boucles décrites ci-dessus sont des boucles 24 , ou des doubles boucles 12.
Le premier tour, représente l’Origine Absolue, le deuxième ,l’0rigine Relative. Ceci permet à la boucle d’être parcourue dans les 2 sens)
Voila donc le sens des « nombres twists » dans lesquels sont inclus les nombres premiers :

- Ce lien de
l’Origine peut être représenté par l’une ou l’autre des 3 boucles dans sa
complétude, ou par leur
lien :
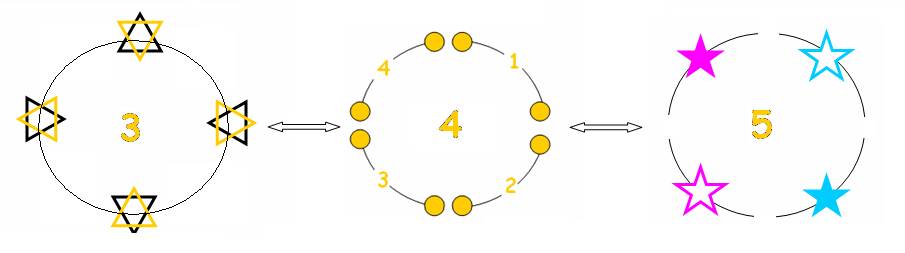
C’est ce qu’exprime à sa façon la relation du triangle de Pythagore 32 + 42 = 52 qui a été au départ de mes réflexions.
Dans cette relation est contenue la notion de 2 réciproques perpendiculaires, récurrente dans mon travail.
Les ondes électromagnétiques en sont un exemple
(Les façons d’exprimer la nature en mouvement de l’Origine , changeant toujours , toujours nai- (ss)-ant ou « néant » , sont …infinies.
J’en ai écrites de nombreuses…
(elles peuvent être
constestées !) , car il
sera sans doute difficile d’en voir la cohérence tant qu’on
n’a pas atteint le « principium ».)
Si on regarde les 3 boucles comme les « contenants » des unités 3, 4, 5 , on remarquera qu’ils sont de 3 natures :
On voit tout de suite la différence entre fermé et ouvert… mais il existe un troisième type…il pourrait être dit de façon paradoxale « fermé par des trous-manques »
La boucle apparaît continue, quantifiée… et liée (par les manques).
Je peux exprimer plus clairement ce paradoxe par un schéma, qui s’explique par l’Evolution de l’Origine :
L’Evolution voit l’Origine comme le LIEN qui unit les opposés.
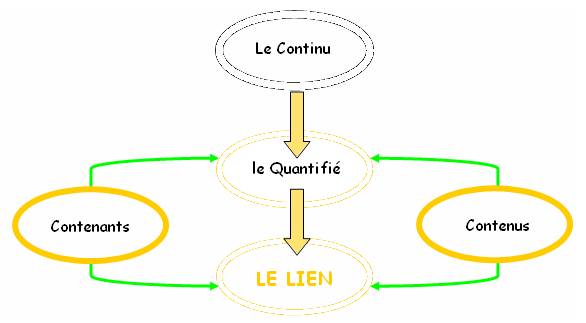
La nature triple de l’Origine , (continu-quantifié-lié) ou celle des 3 boucles (continu-quantifié-lié) dans leur lien peut être représentée par une image :

La lecture de cette image est double. Elle représente :
- le lien entre continu et quantifié
- le lien entre contenu et
contenant
Le lien assure
l’Unité de l’ensemble qui est l’UNITE DECIMALE
Remarque : j’insiste sur le paradoxe de ce chapitre : toute mon étude est faite sur l’étude d’une suite « qui manque », de multiples de 6 qui manquent dans cette suite…qui construit un « lien- qui manque » : il faudrait voir l’ image « en négatif » ! :

Seuls les « nombres Twists » qui sont créés par la dissociation de ces multiples de 6, (ou cause de leur manque), « existeraient » ?