Nature et représentation du nombre
· Quelques observations
Le nombre se définit comme :
-
quantité
![]()
c’est la « quantification » du nombre
- longueur (image d’une corde dont on ajoute des segments), le nombre est représenté par une distance ou longueur
Le nombre est
alors représenté comme une grandeur continue
La corde a 2 extrémités et est formée de segments- « cordelette-distance » qui s’ajoutent : le nombre est la longueur de la corde
Les cordelettes de longueur 1 s’ajoutent pour donner la longueur de la corde
On peut imaginer les segments liés par des « nœuds »
une longueur N, formées de N segments a 2 extrémités et N-1 « nœuds »

- rang (on compte les nœuds en suivant la corde)
Le nombre de nœuds est considéré comme une quantité
Ces représentations sont liées…
mais…
Peut-on avoir UNE représentation cohérente unique?
On peut noter que si on joint les 2 bouts en formant une boucle , le nombre est représenté par la longueur de la corde et par le nombre de nœuds .
(classique problème des « intervalles »). Il existe alors une cohérence
Mais on n’a plus d’ origine à la corde, pour considérer le nombre comme rang !
- Une autre représentation peut être prise en compte :
La longueur de la corde fermée représentation continue du nombre est contenant , d’un contenu-quantité représenté par le nombre de noeuds
·
Nouvelle hypothèse pour
une construction du nombre
Construction :
Le nombre est un contenant , qui définit son NOM
, qui est aussi le rang
Le contenu se définit comme suit :
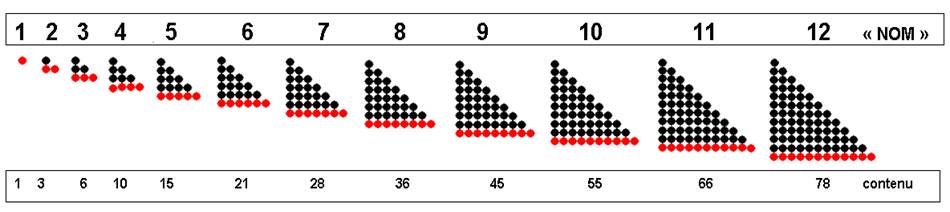

Le nombre se forme en ajoutant au
précédennt, sa valeur-quantité « classique » .
On note ainsi par exemple que la totalité du contenu de 9 est 45, le contenu de 10 est 55…
· Identités remarquables
On remarquera alors que la somme de 2 contenus consécutifs est égale au carré du second nombre
Ceci est représenté sur le schéma ci-dessous ( exemple : somme 10 +11 et 11+12) et par des flèches sur le schéma que j’explique ensuite:
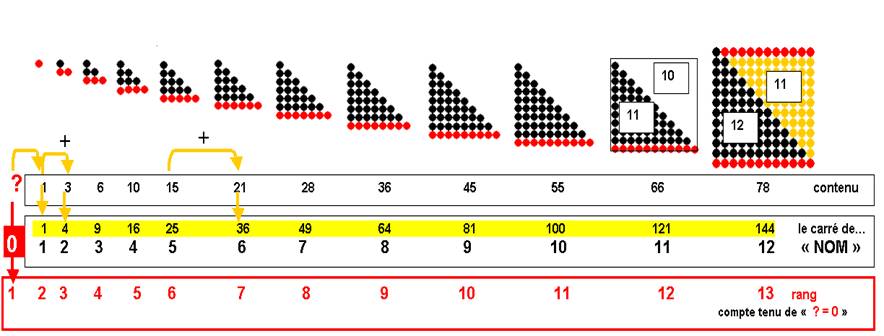
Exemple : (j’écris [ ] , pour « contenu de »)
[1] + [2] = 1 + 3 = 4 = 22
[5] + [6] = 15 + 21 = 36 = 62
… et aussi
[11] + [12] = 66 + 78 = 144 = 122
Pour écrire le carré de 1, selon cette même relation il est nécessaire d’introduire un ZERO tel que [0] + [1] = 12
La présence de ce ZERO change le rang des nombres, celui-ci ne correspond plus au « NOM »initial.
Compte tenu de ce nouveau rang (en rouge), on pourra écrire :
[11] + [12] = 122 = 13
et par
suite :

L’écriture simplifiée (rouge) représente le rang et le contenu
Je conserve ci-dessous la couleur pour notifier le rang :
… mais il apparaît un rang origine… antérieur !… qui définit le ZERO

La suite de Fibonacci se déduit de cette définition : ( ou cette définition explique la suite de Fibonacci qui a été introduite déjà dans « Fibonacci et le principe ZERO »
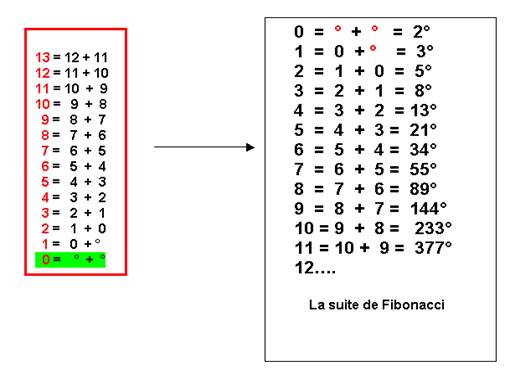
Cette suite n’est pas seulement une construction de l’esprit, elle existe dans la nature…
L’hypothèse de construction de départ est ainsi validée
Elle a d’autres conséquences « remarquables » : cause des identités remarquables :
-
Pour 2 nombres consécutifs : la somme
des nombres est égale à la différence des carrés
-
-

Exemple : 7 + 8 = 64 - 49
- Si les nombres ne sont pas consécutifs
Exemple :
7 + 4 = 11
72 -
42 = 49 -16 =33
7- 4= 3
7 + 4 = (72-42)/(7-4)=
33/3 =11
(différence des carrés : distance)
La somme des nombres est égale à la différence des carrés
divisée par leur distance
Cette relation est valable quand la distance est 1 ( nombres consécutifs)
C’est l’ identité remarquable :
(a+b)(a-b) = a2-b2
L’identité remarquable utilise l’unité duelle de la nature du nombre (quantité quantifiée ou longueur continue)
… et traduit le lien remarquable dans un couple de nombres
Que se passe-t-il à l’origine ?
On verra apparaître sur le schéma ci-dessous que je décris, la définition du ZERO déjà apportée par Fibonacci plus haut :
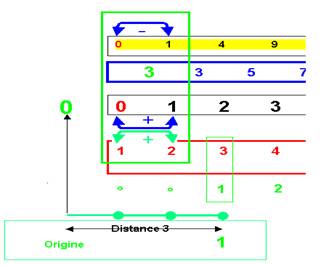
On applique cette fois l’identité remarquable au nombre défini par le rang (nouveau en rouge)
Cette identité est représentée en vert :
La somme des nombres est 1+ 2 = 3
La différence des carrés correspondants est 1 – 0 = 1
On doit donc avoir la condition 1 = 3
Ceci se traduit de 2 façons :
- une nouvelle origine ZERO en vert
- elle est telle que la distance de l’Origine à 1 ( Nouveau départ en vert) est 3
- ce 1 correspond au 3
Toutes les « confusions », sont ici éclairées …
On peut dire aussi qu’elles ont pour cause 1 = 2, le 1 initial est au 2e rang
Tout existe à la fois …
Nous allons préciser encore l’usage de nos nombres…
Par adjonction d’un nouveau ZERO, le nombre-rang est décalé …
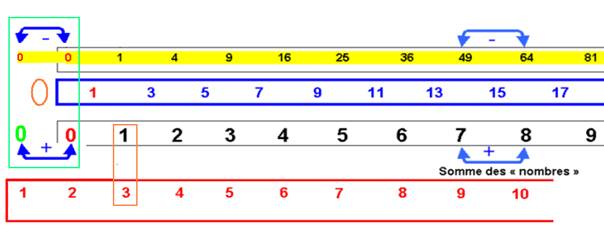
… et le 1 originel est au rang 3… la
distance du 1 à l’origine n’est plus que
2 !
(ceci est en parfaite cohérence avec une partie importante de mon travail initial à partir des triangles rectangles qui démontre l’existence de tiers qui sont aussi moitiés !)…
· La suite des nombres

L’étude précédente et la notion de contenu et contenant nous conduit à cette nouvelle vision :
Considérons le 1 initial comme Grand Contenant vide , ou contenant du Zéro
Ce Grand Contenant apparaît dans la définition de chacun des chiffres, (dessiné en noir ci-dessous)
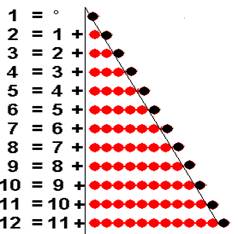
Une rapide observation montre que chaque chiffre est somme de 2 représentations du chiffre précédent
On peut l’écrire de façon plus précise :

Chaque nombre est contenant de 2 formes du précédent :
Ainsi plus simplement par exemple :
9 = (8 + 8) + 1 (le contenant)
( NOM + quantité)
= [ 8 ] [contenant du Contenu : NOM + quantité]
le Nombre est alors : NOM= contenant= contenu= quantité= rang (après une origine triple)
Le rang absolu du 1 serait 4 ! il est « notre 2 » et se trouve à la distance 3 de l’origine) (voir ci-dessous)
Avec la seule condition 2 = 1… toute cohérence est établie !
