10/05/16

OUI MAIS … Pourquoi ?

« Les nombres se décomposent en facteurs premiers  »

novembre 2022 : La REPONSE est une conséquence directe de la Révélation du Secret des nombres premiers.

Mais la beauté secrète de la structure des nombres et du Zéro que nous utilisons , décrite dans ce chapitre en est à la fois Cause et Conséquence.

Nous avons appris que les nombres se décomposent en produit de nombres premiers.

…mais quelle est la structure cachée des nombres qui crée cette propriété mathématique ?

J’ai montré que :

« Le (carré-1) d’un nombre twist est divisible par 12 » et tout nombre twist est un produit de nombres premiers

- le (carré-1) d’un nombre est un multiple de 12 , veut dire que si on enlève 1 au carré du nombre, on obtient un multiple de 12 :

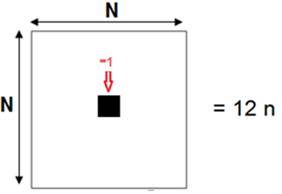
Le carré 1 qui manque , est le lien invisible entre N² et 12n : si on « ajoute » ou n’oublie pas ce lien, on pourra écrire :

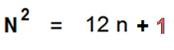
Le nombre N apparait ici dans la complétude de réciprocité Contenant-Contenu :

- 1 est le Contenant, la boucle 12 : « la BOUCLE »

- n est le nombre de tours sur la boucle.

Ici est mise en lumière la confusion usuelle entre contenu et contenant : on oublie le contenant .

Le nombre N représente à la fois contenu et contenant :

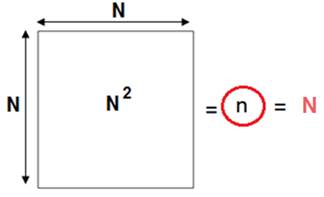
‘le sac de billes contient N billes’ : c’est aussi la réciprocité continu -quantifié.

Le sac est assez grand pour contenir un nombre quelconque de billes : c’est le Grand Contenant que l’on oublie… sa simple prise en compte a permis tout le développement de « la théorie de la réciprocité »

Le nombre N est donc un couple de réciproques, que l’on peut écrire (N,1) .

Chaque contenant N est le Grand Contenant, N=1. Le nombre N est donc le Couple (N,N)

Nous avons vu que la relation « d’amour» d’un couple-nombre est la multiplication : NxN =N²

Cette relation représentée par le carré est la relation de 2 réciproques mathématiques perpendiculaires ( Pythagore et le produit vectoriel apparaissent là)

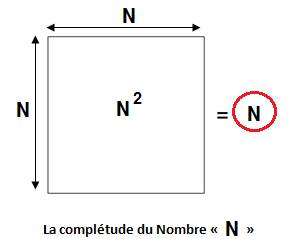
Deux représentations réciproques du Nombre dans sa réalité protomathématique

N = N² = 1 = 12n+1

Octobre 2021 Remarque : la formule ci-dessus n’est ici montrée que pour les nombres twists « T » qui ne tiennent pas comptent des multiples de 2 et 3.

Mais on utilise dans le paragraphe suivant leur propriété d’ enroulement sur la boucle-12, qui va donner la structure cachée de nos nombres:

o La Structure du NOMBRE et la BOUCLE

Le Nombre peut se représenter avec l’unité 12, qui sera « LA BOUCLE » dont nous avons rencontré les états de réciprocité :

o Les nombres-twists s’enroulant sur cette boucle avec l’unité 6, ont donné la première approche des nombres premiers, en position 1,5,7, et 11. (l’enroulement peut se faire dans les 2 sens) :

Représentation de 12 tours

Chaque nombre 1 2 3.. correspond au nombre de tours sur la boucle

o La présence de deux zéros dans la série 0 0 1 2 3 4 5 6 7 8 9….  permet de définir le zéro de « notre » série des nombres : 0,1,2,3, 4… ce premier tour de la boucle,la boucle initiale, est le Grand Contenant Zéro .

La boucle origine contient les autres. On peut aussi la voir comme le support sur lequel s’enroulent les tours suivants :

Chaque nombre correspond alors au nombre de tours sur la boucle et la boucle initiale s’ajoute à chacun des nombres : c’est l’origine de chacun des nombres.

o L’existence de 2 zéros à l’origine se retrouve au niveau du NOMBRE :

Par la construction de 12 tours (l’unité se reproduit au niveau suivant), on voit ici se dessiner 3 systèmes pour décrire les nombres :

-système 12

-système 11

-système décimal

Les 3 sont très liés… et justifieront les résultats que j’ai appelé « protomathématiques » dans le chapitre suivant.

L’enroulement sur la boucle se fait dans les 2 sens :

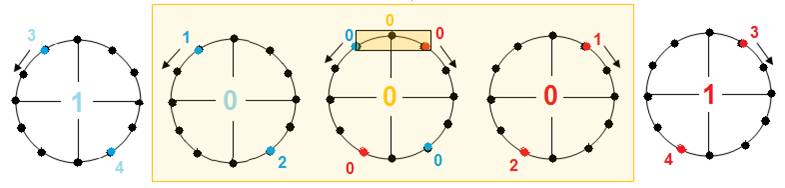
o LA BOUCLE

Lien entre les 2 suites réciproques, elle s’est révélée comme un manque dans l’étude des nombres-twists que j’avais faite

Le lien entre les 2 zéros, transforme LA BOUCLE en boucle-10 : le lien « qui manque » ( 2 points disparus) est énergie de l’origine

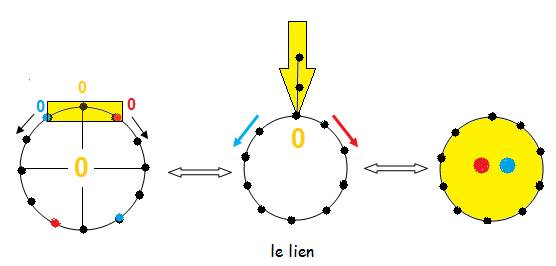
Les 2 sens peuvent s’enrouler alors à partir d’une même Origine:

« La BOUCLE » inclut deux niveaux « cachés » :

2

10

Les nombres qui s’enroulent sur cette boucle unique dans les 2 sens, se définissent simplement à partir des 3 niveaux de ZERO qui sont aussi UNITE.

La description de cette structure est « protomathématique » et les propriétés mathématiques en découlent.

Cependant , la présence liée des 3 systèmes qu’ils utilisent (base 10,11,12) amènera quelques « confusions mathématiques » qui pourront s’éclairer à l’origine protomathématique.

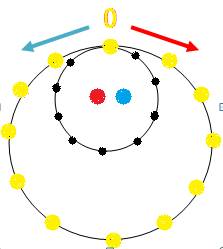
Les 3 niveaux du Nombre ZERO

Ce Zéro est la première boucle parcourue dans les 2 sens, ou vue à l’endroit et à l’envers à la fois.

A partir de là, le nombre de tours définit le nombre.

Suite