La
numération première
Les nombres premiers
Si on écrit les nombres dans 12
colonnes, à part 2 et 3, les nombres premiers se trouvent
dans les colonnes 1, 5, 7, 11 :
(en colonne 2,4,6,8 se trouvent les
multiples de 2 , en colonne 3,6,9,12 se trouvent les
multiples de 3 , qui donc ne sont pas premiers)
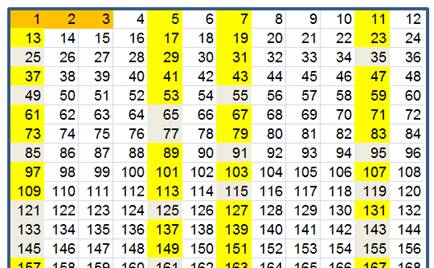
Les nombres premiers (jaune), font partie des nombres
des colonnes 1,5,7,11.,que pour d’autres propriétés, j’ai appelé les « nombres twists ». Je les désignerai ainsi, dans la suite, par
commodité.
On
peut considérer une « symétrie »
autour du 6 ::
les nombres twists sont de la forme : 6x+1 6x-1 6x+5 6x-5
leur carré : 36x2+12x
+1 36x2-12x +1 36x2+60x+25 36x2+60x+25
leur
carré -1 : 36x2+12x 36x2-12x 36x2+60x+24 36x2+60x+24 est divisible par 12 (et même par 24)
Le carré de tout nombre twist se trouve dans la colonne 1 .(1 modulo 12)
Donc le carré des nombres est
(multiple de 12) +1, ou le (carré -1)
des nombres twists est divisible
par 12
Le tableau ci-dessous montre même la divisibilité par 24 :
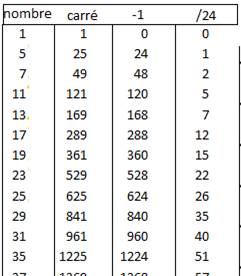
remarque: la forme
carrée est donc adaptée pour une représentation des nombres, de la quantité
qui les constitue, avec l’unité que j’ai définie au chapitre
précédent :
J’ai utilisé un petit carré quantum, que j’appelle « karum »
(k)
et défini une nouvelle unité :
1® = 24 k
Représentation des
nombres-twists :
Sur le schéma ci-dessous, les nombres twists ( nombres des colonnes (1,5,711)) sont représentés, par leur longueur,(en vert), et leur carré :
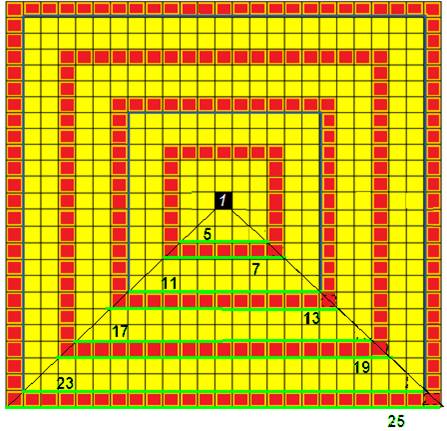
·
Dans ce
chapitre nous étudions la représentation par les longueurs :
On remarque qu’elles peuvent être
décrites par l’ensemble de 2 suites :
1 , 7, 13, 19, 25…
5, 11,17 ,23 …
Ce sont des séries algébriques de raison 6
Dans l’habitude de la numération, de la connaissance que nous avons des nombres :
ces 2 suites semblent commencer respectivement en 1 et -1

Les 2 séries diffèrent par l’origine
qui est choisie pour la numération :
Avant toute numération, existerait une origine « ZERO », et une suite unique que je peux représenter par une succession de « 6 kara » :
![]()
Paradoxe :
En COHERENCE avec ce que nous CONNAISSONS DEJA des nombres, mais en S’AFFRANCHISSANT DU DEJA-CONNU,
peut se déduire la NUMERATION PREMIERE :
A partir de l’étude des nombres
premiers, a été mise en évidence l’importance de la « quantité 24 »
L’ensemble de 24 kara, que jai appelé unité ®, permet alors de construire cette NUMERATION:
Elle commence à l’origine unique
que nous appelons « ZERO », elle utilise l’élément « 6 kara», que
j’appelle « unité 6 ».

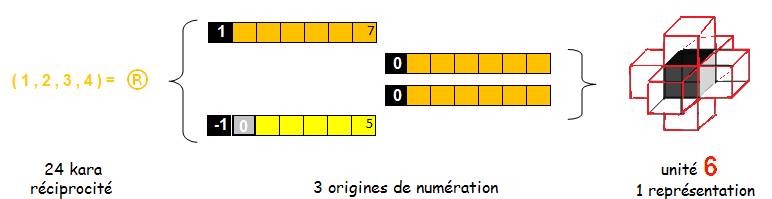
Dans l’unité ®, se définissent 1,2,3,4, par l’unité 6, que 1=2=3=4 et que la somme 1+2+3+4= 1®
Ceci constitue les propriétés de
réciprocité du quaternion (1,2,3,4) = ® , dans la cohérence de « la
théorie de la réciprocité » que j’ai développée dans mon travail.
On peut considérer pour les nombres 1,2,3,4 ainsi définis par l’unité 6,
trois origine de numérations :
- l’origine 1, a été mise en
évidence par les colonnes 1 et 7 : elle définit ces colonnes
- l’origine -1, par les colonnes 5
et 11
- l’origine 0 est celle de notre
numération
Si on représente l’unité 6 avec une origine , elle correspond à un « élément 7 » :
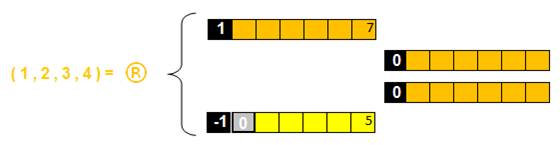
La QUANTITE est cependant
toujours indépendante du point origine qui permet de la « mesurer »
·
La représentation par les carrés au chapitre suivant fait évoluer
et complète cette numération première.
Elle donne en particulier une forme unique aux trois représentations :