Les
nombres premiers, témoins de la
construction du système décimal ?
· Si on écrit les nombres dans 12 colonnes, à part 2 et 3, les nombres premiers se trouvent dans les colonnes 1, 5, 7, 11 :
(en colonne 2,4,6,8 se trouvent les multiples de 2 , en colonne 3,6,9,12 se trouvent les multiples de 3 , qui donc ne sont pas premiers)
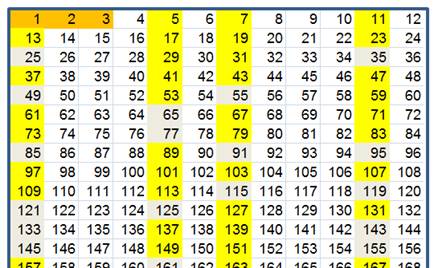
Les nombres des colonnes 1,5,7,11 , sont tous multiples de 6, plus ou moins 1.
On peut donc remarquer que les nombres premiers sont de la forme 6n+1 ou 6n-1 .
On peut aussi considérer que la suite des nombres est enroulée sur un cylindre à 12 positions.
Le premier tour est représenté ci-dessous, sous une forme qui nous est familière : celle du cadran d’une horloge
On a l’habitude de
voir les 12 points dans un enroulement
croissant « dans le sens des aiguilles d’une montre »
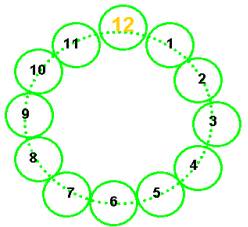
Cette vision est très limitée !
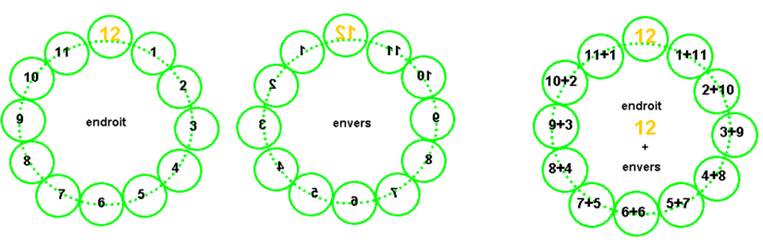
Si on considère à l’endroit et à l’envers, les relations entre croissance et décroissance des nombres et le sens de parcours de la boucle, on obtient quatre boucles
Je les représente ci-dessous dans une paire de double-boucles « twistées »au point 12
Ceci traduit la particularité du point 12 qui est DOUBLE dans la superposition endroit-envers ci-dessus. Les autres points ont une somme endroit-envers égale à 12 ;
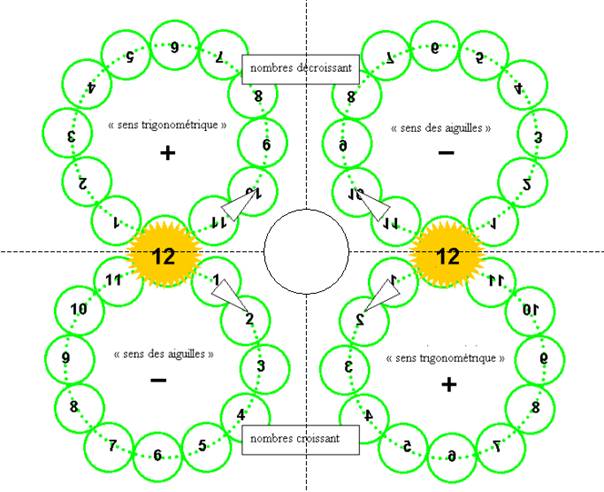
Les propriétés de symétrie et de superposition de ces boucles constitue ce que j’appelle leur « RECIPROCITE »
Endroit et envers constituent une paire de réciproques
Dans la représentation ci-dessus, 12 est origine et fin de chacune des boucles
Dans la suite numérique , chaque boucle aura son origine et sa fin
La suite numérique s’enroule en double hélice :
L’enroulement dans les 2 sens se décrira cette fois en une paire de 2 doubles hélices réciproques parcourues dans les 2 sens
Voici le tracé
des premiers double-tours où l’on voit
apparaître les nombres premiers
(je rapporte ici quelques exemples que j’ai tracés, on peut ne pas trop s’y attarder quand on a vu le système d’enroulement)
L’ observation de ces doubles-hélices permettra ensuite de décrire leurs propriétés communes
· 1 double-tour
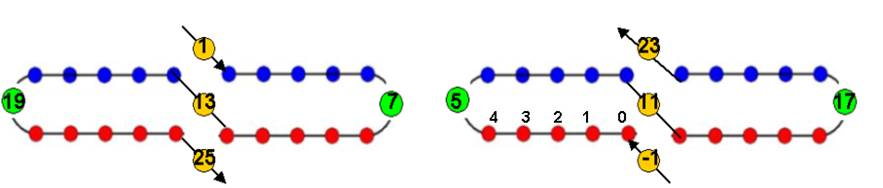
remarques :
13 se superpose à 1 pour fermer la première boucle, la deuxième s’enroule dans l’autre sens et se ferme en 25
Si on considère une origine 0 pour la première boucle, 11 ferme la boucle en se superposant au point précédent –1
12 n’apparaît pas comme point milieu !
·
2
double-tours
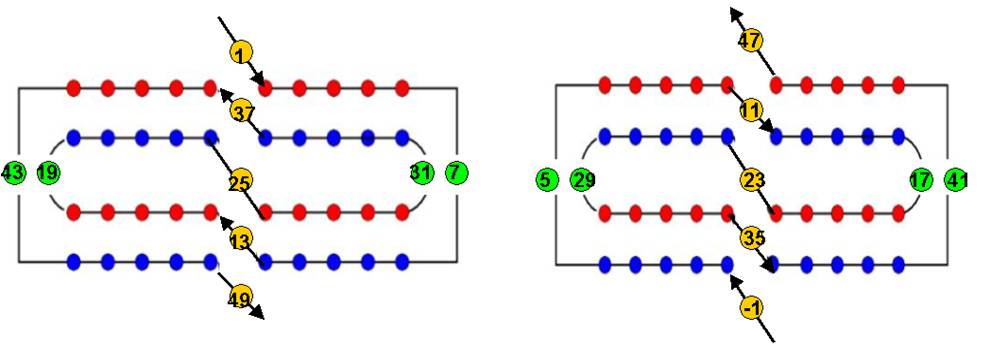
·
3
double-tours
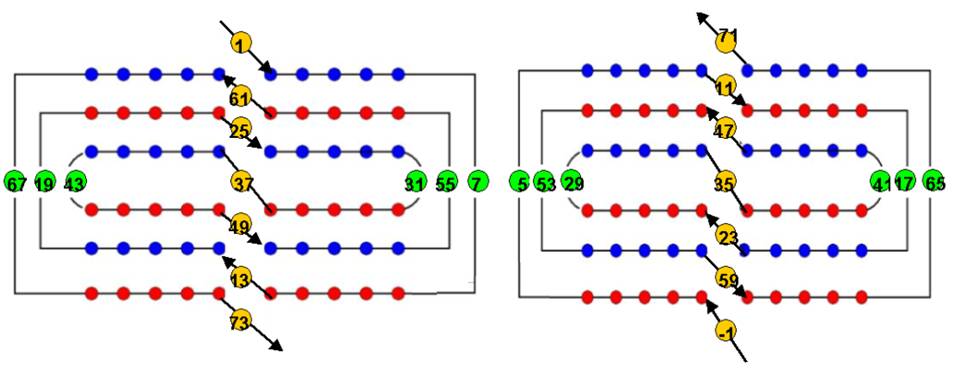
· 4 double-tours
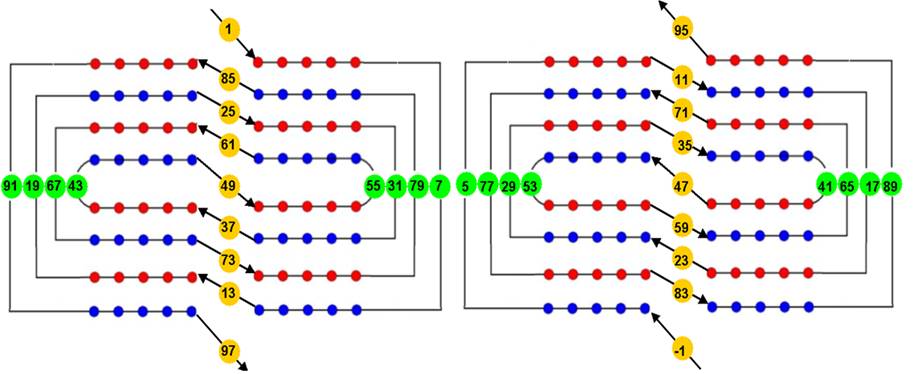
·
5
double-tours
·
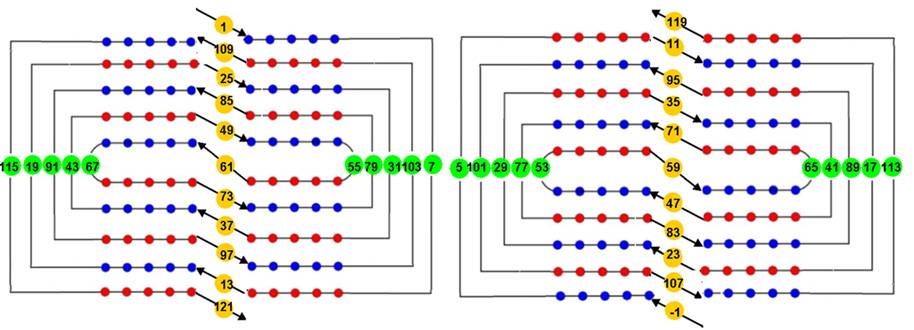
6
double-tours
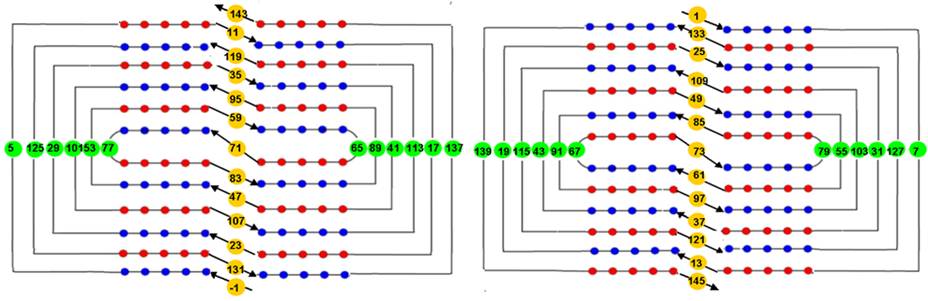
·
7
double-tours
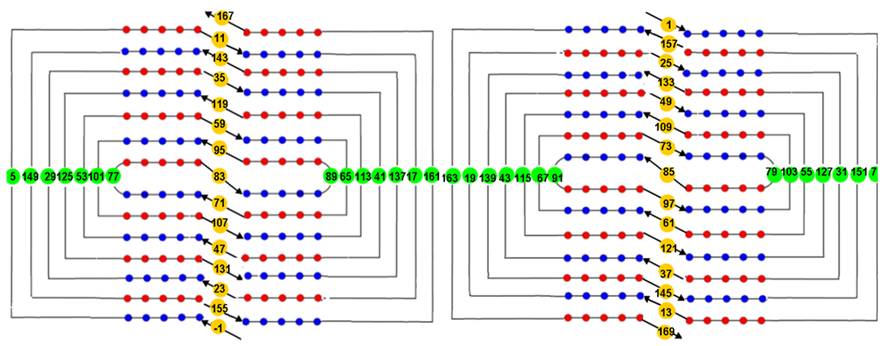
Propriétés de la Double-Hélice
Je montre ces particularités sur un exemple (2double-tours) : il sera facile de les retrouver dans les autres cas.
2
double-tours ou « double-hélice 24 » :
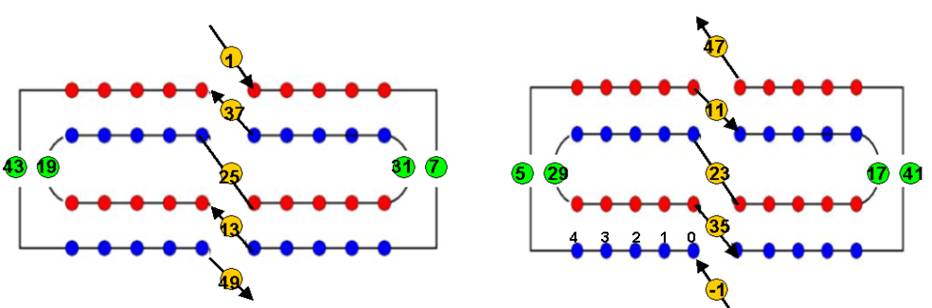
- La double hélice est représentée dans les 2 sens
- Les 2 doubles hélices sont réciproques :
- La superposition des 2 enroulements est telle que chacun des points a un contenu-somme égal ( même ceux qui ne sont pas numérotés ) :
1+47 = 37 + 11 = 43 + 5 =
19 + 29 = 25 + 23 = 31 + 17 = 7 + 41 = 13 + 35 =
49 –1 = 48 = 2 x 24
- Sur chaque enroulement le sens change au milieu que j’appellerai « point –twist » ( 25 et 23 )
Le point 24 serait un « TWIST Virtuel » pour la double-hélice « dans sa complétude »
- Sur un même enroulement, les points symétriquement opposés ont pour somme le double-twist :
43 + 7 = 19 + 31 = 1 + 49 = 37 + 13 =
50 = 2 x 25
5 + 41 = 29 + 17 = 47 - 1 = 11 + 35 = 46 = 2 x 23
- on reconnaît sur les horizontales (en vert) les colonnes du 7 et du 5 du tableau initial
sur les verticales(orange) , la colonne 1 et la colonne 11 qui commencerait à –1
- Tous les nombres des colonnes (1,5,7,11) apparaîtront quand le nombre de tours augmente
Ce sont les « nombres-twists »
« Nos nombres premiers » font partie des nombres-twists
Chaque double hélice peut être considérée comme la réciprocité de 4 boucles fermées
Je représente ici 4 exemples à observer (suivant la taille des hélices, les propriétés peuvent se voir plus facilement)
On notera que dans chacune des réciprocités, les boucles ont respectivement pour origine -1,1,11, 13 et que 12 points sont exclus de chaque boucle fermée.
Un premier travail de description se fera ensuite, qui permettra de découvrir les propriétés communes
Notre but est d’éclaircir le sens , le rôle ou la nature des « nombres-twists » (ou des nombres premiers tels qu’ils nous apparaissent)
-
TWIST 12 – Hélice 1 ou « la double –hélice 12 »
La position particulière des nombres premiers va apparaître dans cette représentation réciproque
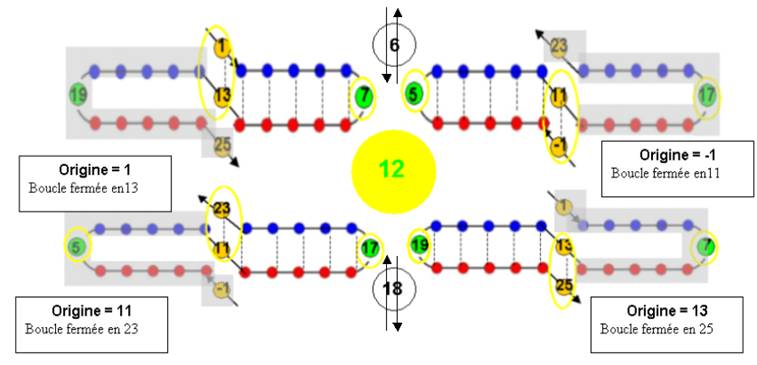
La somme des points liés opposés a la valeur double des points 5,7, 17,19
Ces points sont donc doubles, points de retournement : ce sont des points TWISTS
- TWIST 24 – Hélice 2 (2x12=24)
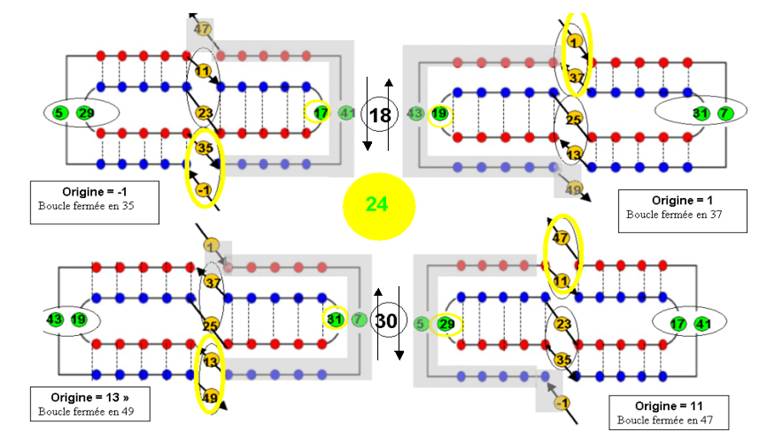
- TWIST 36 – Hélice 3 (3x12=36)

- TWIST 60 – Hélice 5 (5 x12 =60)
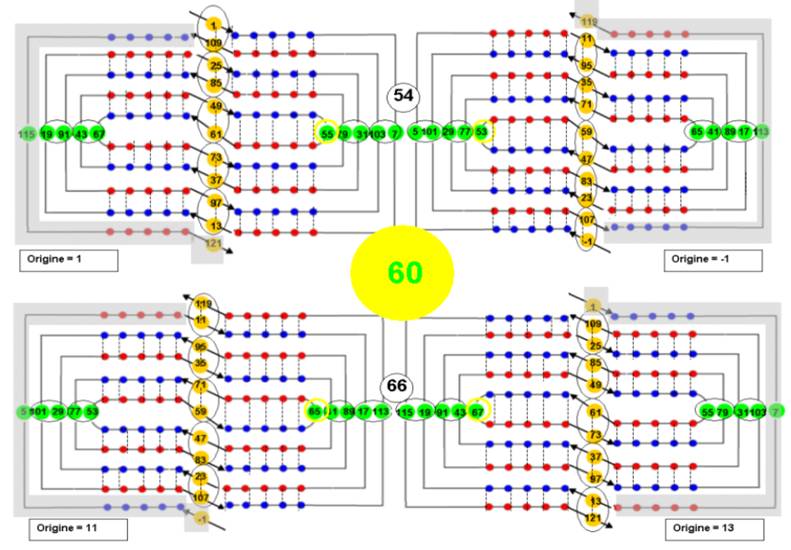
-
Premières
conclusions
-
(
4 boucles réciproques + 12 points qui relient le début et la fin)
Dans chacune des boucles, les points sont liés par paires. Toutes les paires ont la même somme.
La somme de la paire est égale au double du nombre point « extrême ou milieu », qui est Point-Twist, ou de retournement : un nombre twist
Le schéma ci-dessous récapitule les observations des doubles-hélices :
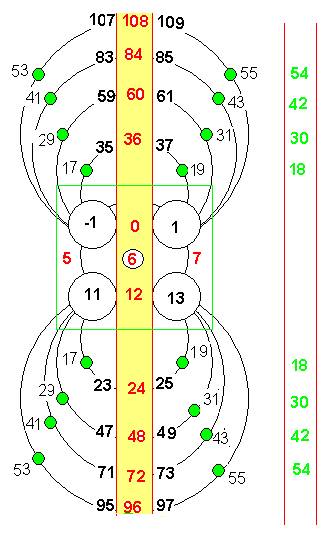
Les 4 boucles de l’Hélice 1, relient les points –1, 1,11,13,
Dans chacune des autres hélices, les 4 points –1, 1,11,13, sont origine d’une courbe qui se ferme en boucle par un nombre-twist (au contact de la colonne colorée) : une paire de nombres –twists encadre un multiple de 12 (en rouge)
Le milieu (point vert) de chacune des courbes et moyenne de toutes les paires opposées de la courbe, est point de retournement nombre-twist : une paire de nombres-twists encadre un « Twist-Virtuel » multiples de 6 (colonne en vert)
Les multiples de 12 (dans la colonne colorée) sont « Twists Virtuels » de chaque double-hélice, ou moyenne des twists de la paire réciproque
Tous les multiples de 6 sont des « Twists Virtuels ».
Ceci se traduit dans la « symétrie » par rapport à la colonne 12 :
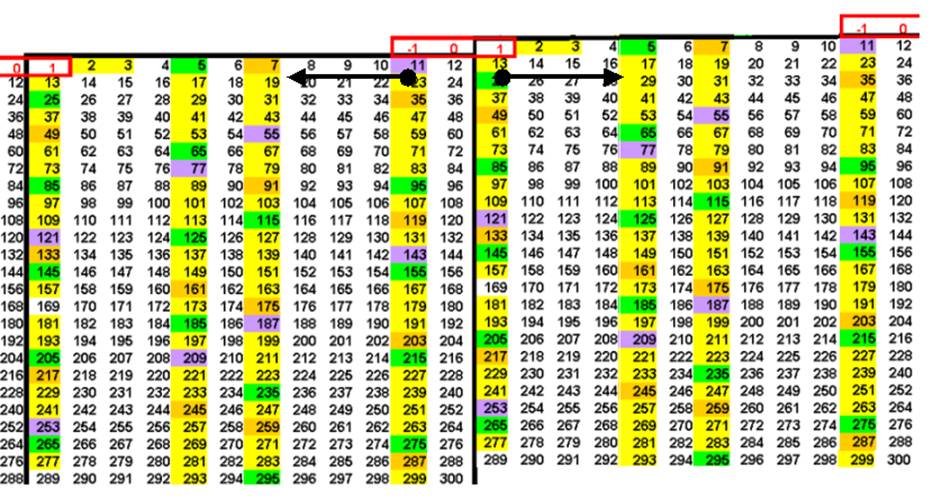
- Cette symétrie montre que l’Origine qu’on appelle zéro est un Twist qui crée 2 sens opposés ou réciproques
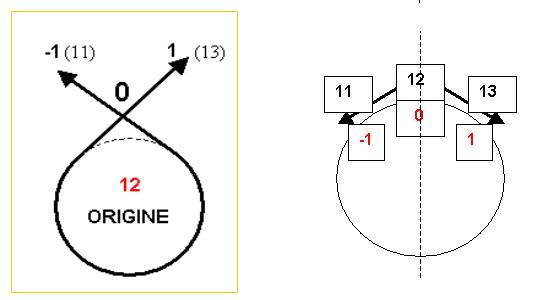
- A partir de cette origine 12, que l’on peut appeler 1, sont également créés 2 autres réciproques : la suite paire et la suite impaire (multiples de 12 dans la colonne colorée ci-dessus)
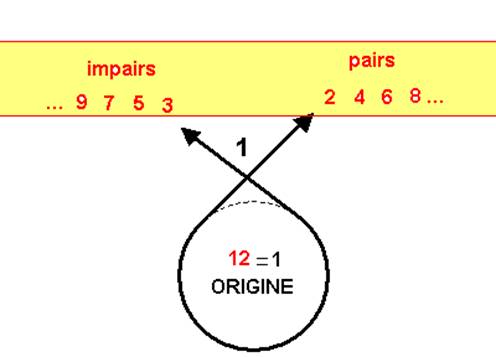
- Deux autres réciproques la fin et le commencement, prennent le sens de -1 et 1, dans une boucle symétrique qui « culmine » au point-twist, point double de retournement qui prend la place du 12 initial
Fin et commencement seraient alors « réversibles » comme endroit et envers !
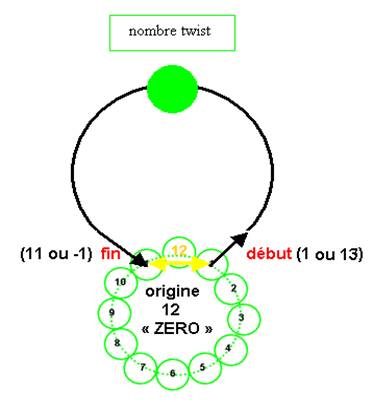
Sens des 12 points cachés dans 4 boucles réciproques :
La boucle 12 est le lien caché qui lie les 4 boucles réciproques :
« elle apparaît » comme les 12 points cachés dans chacune des 4 boucles réciproques
Quel est alors le sens particulier de 5 et 7 ?
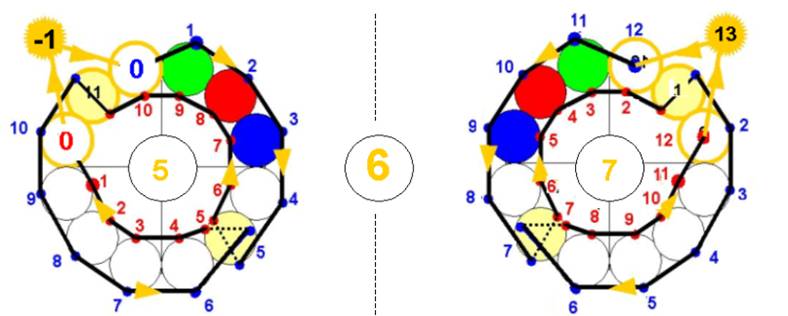
La boucle initiale est elle-même double et parcourue dans les 2 sens : 5 et 7 sont des twist doubles : ils changent le sens de parcours sur la boucle.
Ils donnent leur valeur 10 ou 14 à chacun des points des 2 enroulements réciproques représentés ci-dessus, qui se superposent parfaitement par symétrie (pliage) dans une somme 12
On voit apparaître 2 origines 0 ( dans la suite croissante et la suite décroissante)
1 et 11 sont également des twists : ils font passer la suite des nombres de croissance à décroissance (ou réciproquement)
(1,5,7,11) est la réciprocité Twist première
Ainsi apparaît le Twist Virtuel, symétrie de la colonne 6 :
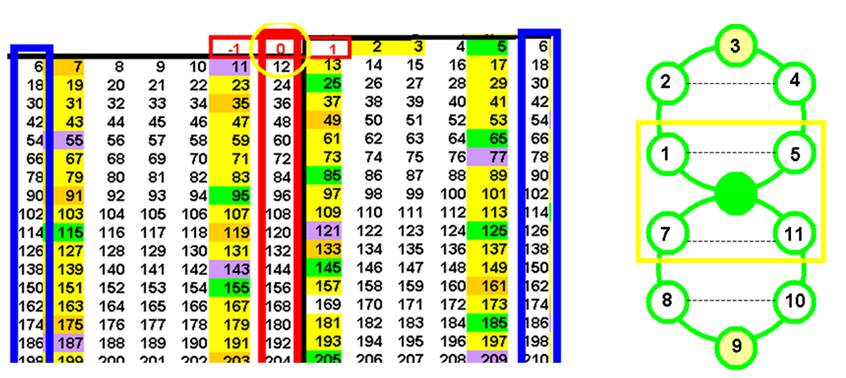
L’enroulement des nombres en « boucle twistée » simple montre la position particulière du quaternion premier (1, 5 , 7 , 11) qui sera celle des points-twists et de « nos » nombres premiers.
Les nombres premiers témoignent d’une structure à base 12, duodécimale, des nombres
On remarquera que les sommes des paires formées (2,4) (1,5) (7,11) (8,10) sont des multiples de 3
3, 6, 9 ou ( 3x1, 3x2 , 3x3 ) sont les nombres twists de cette boucle première : ceci traduit la particularité de la Trinité (1,2,3) ou Unité Trine qui fait que 2 et 3 sont exclus* des « nombres premiers »
La suite montrera que l’existence et la nature du zéro transforment le système duodécimal en système décimal (chap : la boucle 12 et le système décimal)
L’Unité Trine et le Cercle
La « disparition » de 6 et 12 ou le TWIST en 6 et 12 (aux multiples de 6), permet une nouvelle représentation qui « explique » l’unité 60, utilisée déjà par les babyloniens et les 360° du cercle
On notera sur le schéma ci-dessous, le sens des boucles, l’entrelacement de 2 hélices en sens inverse…
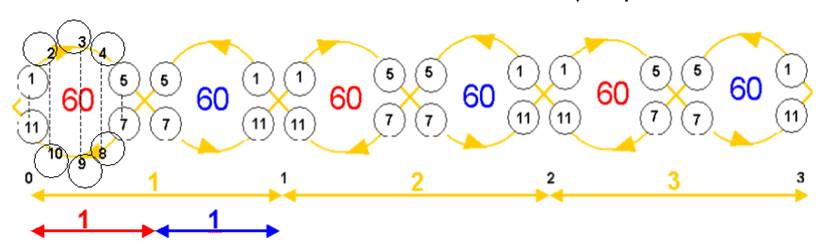
Cette représentation peut être vue comme l’Unité Triple de 3 couples de boucles en mouvement
![]()
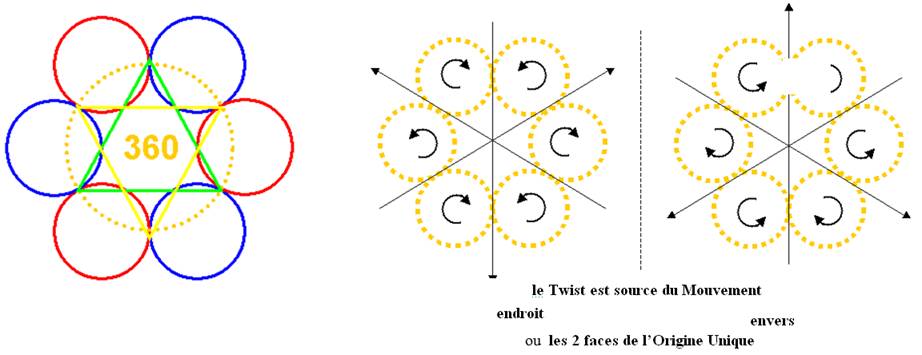
Conclusion : le Nombre crée le Mouvement
Sa malléabilité est Source d’Evolution
(« glissement-mutation »)
Les chapitres suivants vont dévoiler la structure de la construction des nombres que nous sommes entrain d’utiliser …