NOMBRES
PREMIERS et ORIGINE
·
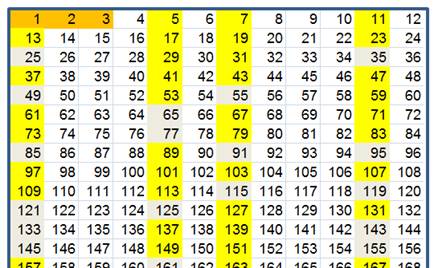
Si on écrit les nombres dans un tableau à 12 colonnes,
les nombres premiers (sauf 2 et 3) se trouvent dans les colonnes (1,5,7,11)
En effet, les colonnes 2,4,6,8,10 contiennent les multiples
de 2 et les colonnes 3,6,9 contiennent les multiples de 3.
.
Les
nombres dns un tableau à 12 colonnes ou enroulés sur une boucle à 12
points
La
boucle peut se développer en sinusoïde ou onde.
J’ai
représenté les nombres de ces colonnes qui contiennent les nombres premiers sur un axe .
Je
les ai appelés « nombres-twists » Tn
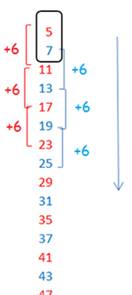
Ils
appartiennent à 2 ondes « réciproques ».
Ces
2 ondes résultent de la
« dissociation paradoxale » d’une Onde Origine qui se trouve ainsi définie.
· Une ONDE
ORIGINE… une vibration
infinie … sans fin et sans commencement –origine… elle se dissocie :
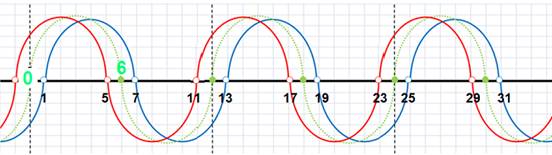
· L’existence des
NOMBRES PREMIERS implique celle d’une NUMERATION et de son point Origine.
Un choix (RELATIF)
situe l’Origine 0 de cette numération .
Les nombres premiers imposent
la longueur de l’Onde Origine , sa période : 12.
· Ainsi
apparait la définition
ONDULATOIRE du NOMBRE :
Le
nombre se définit par sa représentation ondulatoire à partir de l’Onde Origine.
La
période 12 de l’onde Origine décrit le
nombre 6 .
Plus
généralement : le nombre N existe inséparablement de l’infinité de ses multiples, c’est sa nature vibratoire :
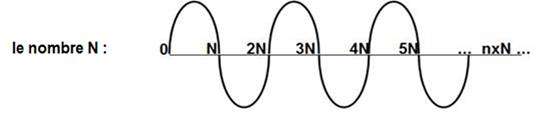
Par analogie avec la
dualité onde-particule, regardons le nombre comme une onde, en
l’associant à ses multiples.
Dans sa propagation, il éclaire progressivement les points de l’axe ….
J’utilise le verbe « éclairer » en référence
à une onde, lumière :
Les ombres, éclairées, deviennent ‘No-ombres’ :
Nombres ...
« Nombre
& Lumière » exprime la nature duelle du nombre QUE et QUI révèle le secret des nombres
premiers :
Les nombres premiers révèlent l’existence
de l’ ONDE ORIGINE de période 12, qui se
voit comme La BOUCLE-12.
Réciproquement, c’est l’existence de
La BOUCLE (où s’enroulent les nombres) qui révèle les nombres premiers.