2
= Origine Transfinie ?
Ce chapitre peut être un peu difficile à suivre… car il décrit l’imbrication des diverses unités… mais il est fondamental car il découvre le nombre @ , que j’appellerai l’@lliance
(Certaines remarques, schémas ou observations peuvent l’alourdir, ne concernant pas directement le raisonnement. Elles font ressortir des propriétés qui intéressent la cohérence de l’ensemble)
La complétude du nombre est transfinie et 2 est Origine : c’est le résultat du chapitre précédent
· J’utilise donc le nombre 2 , je le choisis comme Origine n dans « la belle formule »
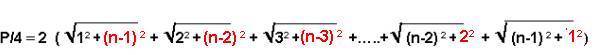
A partir de cette Origine, la formule P/8 devient :
![]()
(on note que 2-1 = 0 , 1 étant inclus dans le cercle Origine : c’est le résultat du chapitre précédent, qui redonne la condition de réciprocité 1= 2 )
La formule P/8 peut être représenté géométriquement, par les hypoténuses des triangles rectangles et l’utilisation de la symétrie de réciprocité ci-dessous :
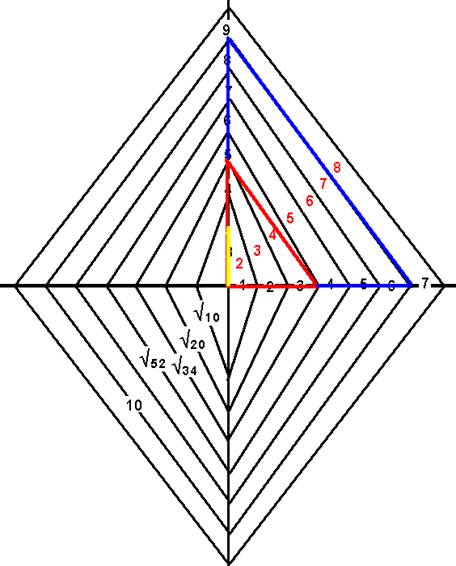
Observation :
En rouge j’ai placé le chiffre intermédiaire tel que (n-1) = [ n + ( n-2 )] /2
Je remarque que la construction commence à 2
2, le Transfini, est l’origine de ma construction .
J’ai noté sur mon schéma, la longueur des hypoténuses
Je m’aperçois que pour n
= 8 , on a un nombre entier, bien particulier 10
Cette hypothénuse est celle du triangle bleu qui est semblable au triangle de Pythagore (3,4,5) (en rouge) dans le rapport 2
Ci-dessous, je complète les triangles rectangles, par « la moitié qui manque » à leur « complétude-rectangle » .
Les rectangles successifs sont tracés sur le schéma ci-dessous :
Je vois apparaître la « symétrie » de 2
réciproques perpendiculaires
Elle est incomplète, j’en détermine donc le centre :
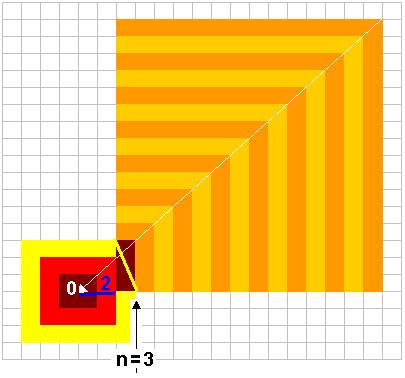
Les hypoténuses des triangles commencent au 3, après le 2 qui est la distance depuis le centre de symétrie réciproque
Je les trace dans l’espace de réciprocité ainsi centré ci-dessous :
Après l’Origine 2 qui est le Zéro, 3 est le 1-départ, ce
Par une similitude de rapport 3, je trace les hypoténuses semblables aux précédentes dans un rapport 3 : elles sont alors centrées par rapport au centre de réciprocité
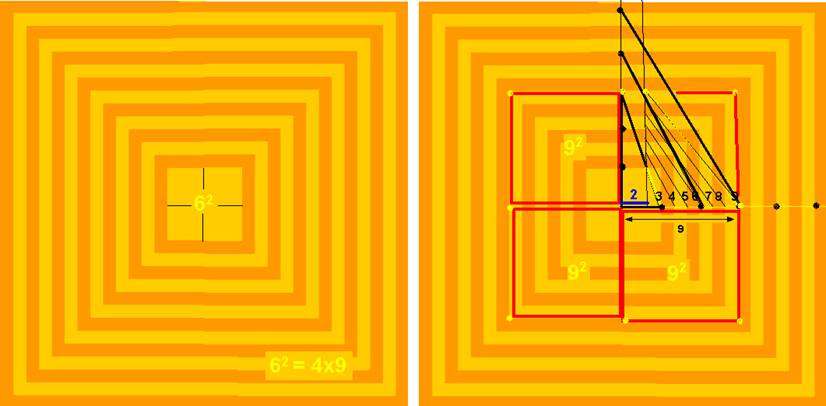
Elles définissent la nouvelle unité (en jaune) 1 = 3
x 1
De la même façon, on pourrait introduire une nouvelle unité 1 = 3 x 1 = 9 x1 elle correspondrait à une distance au centre égale à 9 unités du départ ( ce qui correspond à 7 sur la graduation du schéma : distance à partir de l’origine initiale 0
(ceci est détaillé plus bas )
Remarques sur l’origine des nombres et leur nature :
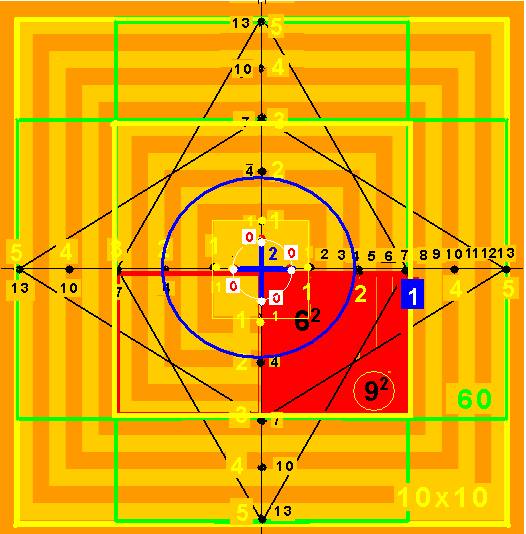
Les divers niveaux des nombres et leurs relations sont représentés sur le quart de la figure que je reprends ci-dessous :
La différence entre rang et distance contient déjà le décalage introduit par une origine ( je le montre en graduant abscisse et ordonnée)
- L’abscisse horizontale (en gris) considère le nombre comme un rang à partir du centre (coin supérieur gauche)
- L’ordonnée verticale (en gris) exprime la distance depuis l’origine-centre 0
Les « confusions » possibles sont alors soulignées par des correspondances sur le schéma
Ce schéma est important car il permet aussi de voir des correspondances qui sont utilisées par « les mutations » ou glissements de « la logique protomathématique » difficilement explicables et acceptés par un esprit « scientifique ».
Ce sont ces subtilités qui entrent dans la définition des différentes unités et qui amènent jusqu’au questionnement sur la nature de l’univers…construit sur quelle base ?… 10…11.. 12… ?….
Toutes les bases sont imbriquées
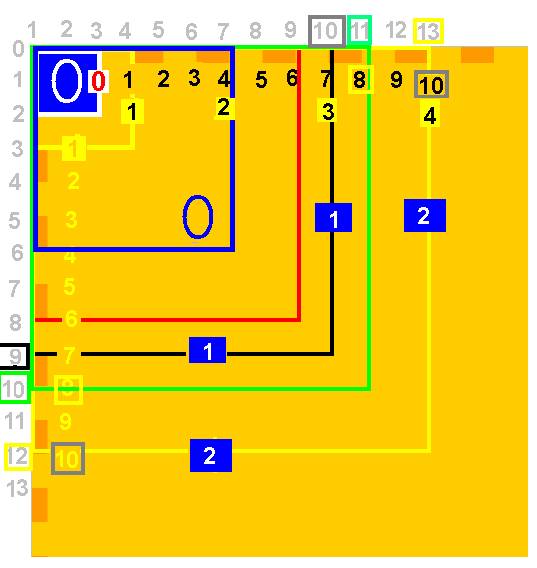
Lecture du schéma :
On retrouve en carré bleu l’0rigine Zéro et la série en noir initiale 1 2 3 4…, nos nombres qui commencent au 0
Au dessous la série jaune, commence au 1 de départ avec une valeur de l’unité 1 = 3 ( le pas vaut 3 : distance)
Le 2 de cette série correspond à une nouvelle origine ZERO, qui donnera naissance à la série bleue qui commence à son 3 (jaune)
Le 2 bleu, sera lui-même origine d’une autre série dont le pas aurait la dimension 6 de départ…
La place particulière du 3 est mise en lumière:
L’origine semble toujours fuir et se recréer… la généralisation est étudiée ci- dessous :
Existe-t-il une
origine et un pas unique pour la série des nombres ?
· La fuite de l’Origine :
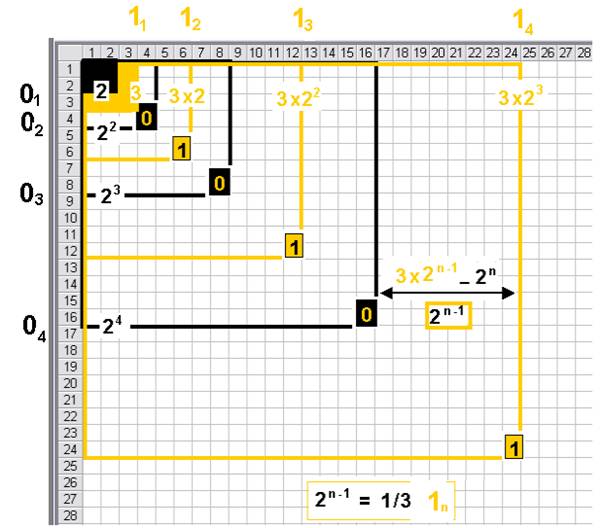
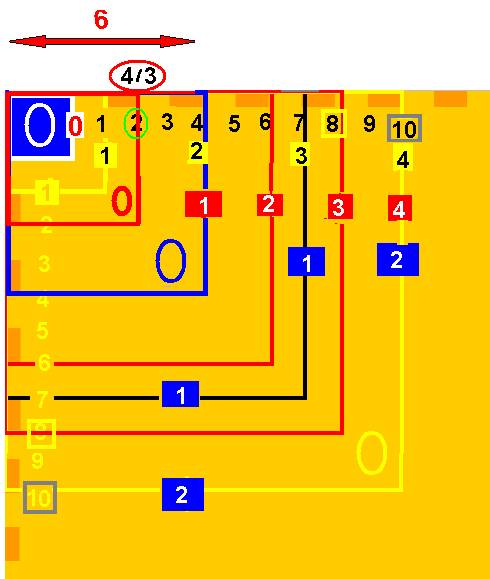
Sur ce tableau (ci-dessous) , je représente les 0 (qui sont des puissances de 2) et les unités 1 correspondantes qui sont multiples de 3 :
Puis-je alors écrire que :
Les zéros sont les puissances de 2 et l’unité est le
triple zéro !
Je calcule la distance entre le nième Zéro et le 1 correspondant :
Le nième zéro est 2n , et le 1 correspondant est 3 x 2n-1
La différence entre
le nième zéro et le 1 correspondant
est 3 x 2n-1
- 2n
= 2n-1( 3-2) = 2n-1 : c’est la valeur du zéro précédent.
(0 et 1 sont affectés d’un indice qui exprime leur rang) :
![]()
Existe – t-il un dernier 2 qui créerait le ZERO- Origine de départ , comme un retour en boucle à l’Origine ?
Je prends cette hypothèse, qui s’est déjà confirmée au cours des chapitres
Si la boucle se ferme 1n
= 11 = c’est la valeur 1 du premier 1
Avec cette valeur 1
2n-1 = 1/3 x 1n = 1/3 , la différence entre le nième zéro et le nième 1 est :1/3
2n-1
permet de calculer le nième zéro qui est
2n
2n
= 2/3
Cette position est celle du premier zéro , le zéro de la série de « nos » nombres qui commence par 11 = 1, que j’ai représenté par : 0
Le nième zéro et dernier zéro 2n
est par définition celui qui est égal au suivant le (n+1)ème :
2n+1= = 4/3
2n = 2n+1
![]() Cette puissance de 2 qui ferme la
boucle est telle que n =
n+1 =@
Cette puissance de 2 qui ferme la
boucle est telle que n =
n+1 =@
@ est par définition le transfini tel que @ = @ + 1
Je choisis ce symbole bouclé ( en cohérence avec le reste de mon travail), pour exprimer cette valeur particulière de 2 :
2@ = 4/3
(Je remarque que cette condition impose aussi que 2 = 4)
Le 2
défini par 4/3 est l’ancien et le nouveau.
Notre 2 (entouré en vert) est 2@ !
2@
= 2 donc @
= 1 C’est l’expression
du TRANSFINI
Cette valeur va ainsi être celle de tous les nombres car n= n+1=@ a pour conséquence 1=2=3=4=5…
On peut voir cette valeur
· comme le contenant du nombre, qui contient toutes ses parties, le nombre est quantifié.
· comme le lien qui unit toutes les parties pour faire du nombre un seul tout : ce lien peut être appelé « @lliance ou @mour "
La distance entre 1 et 2@ est ce que nous appelons « 1 »
Le 2 = 2@ définit le 1, comme divisible par 3, ou comme distance 3 ( 1 = 3) ce qui justifie le « zéro » qui a été introduit.
La position du 2 donne la dimension 4 au zéro . (la condition n= n+1 impose d’ailleurs 2 = 4).
C’est la dimension du nouveau ZERO : en rouge
Le 1 est alors
redéfini , il a la dimension 6
1= 6
Sur le schéma , il est facile de voir que 0=1=2=3=4 = 6
( ces conditions ont été par ailleurs trouvées aussi dans le chapitre : 0 = 2 1 = 2 1 = 3 2 = 4 1 = 6 )
La série des nombres définie par 2@ est en rouge sur le schéma. Le pas vaut 2 x « 1 » . le nouveau 1 vaut 2 fois l’ancien , ou « chaque chiffre est double »
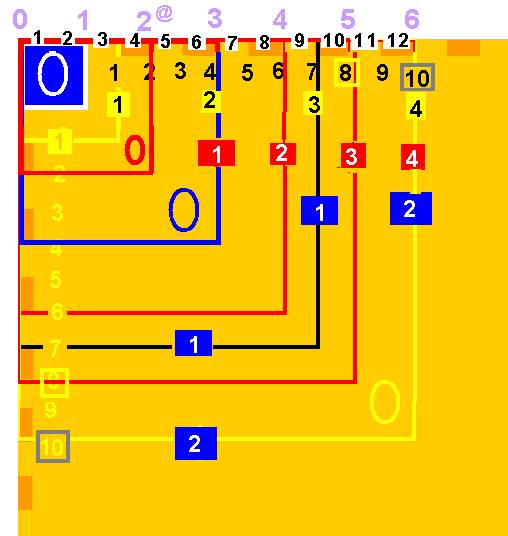
Avec ce nouveau pas, 2@ appartient à une série (en violet ci-dessus) qui commence au Centre-Origine 0, et donne à l’Espace une symétrie sphérique simple à base 6 , que l’on peut voir aussi comme système duodécimal 12 , qui correspond aussi à notre système décimal 10
J’ai longuement étudié le lien de ces 2 systèmes dans mon travail protomathématique : ici il apparaît facilement :
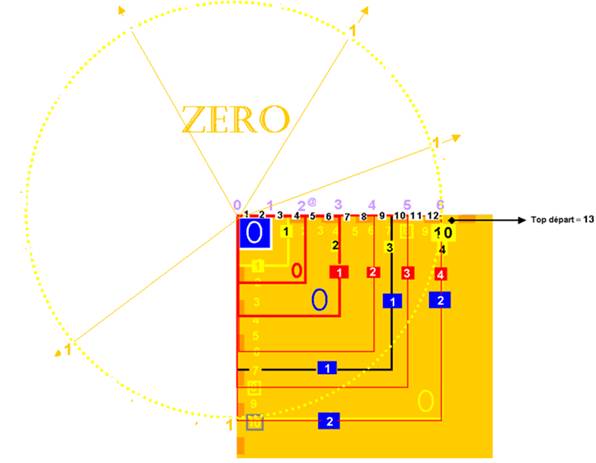
Conclusion :
2@ = 4/3 ou @ = log2 4/3 = 0,41503749927848 …..
2@ définit la dimension et la position
du ZERO Origine Transfinie, qui donne la
position du premier UN et la valeur du pas de la série 1,2,3,…n…
Quand 2@ revient se superposer à 2, on a parcouru un tour, c’est ce qui s’écrira :

la valeur 4/3,
apparaît dans le volume de la sphère et mon étude des pyramides
en donne la cause… ce sera le prochain chapitre)
@, π et… 2 (comme
e qui intervient dans le
logarithme) sont des nombres transcendants, à l’Origine ils ont la valeur
transfinie 1 = 3
Cette
égalité exprime celle de la sphère et du cercle de rayon 1 (volume, surface
,circonférence)
π symbolise cette unité, lien-boucle transcendant l’opposition 0 –1 que représente la vision duelle contenant- contenu ( « la magie du Beau Lien »)
