
Les empilements qui constituent la beauté des pyramides contiennent les séries définies par la structure des nombres et décrites dans la « construction d’une perfection »
Si donc les nombres construisent les pyramides, les pyramides révèlent les secrets des nombres…
C’est ce que découvre ce chapitre
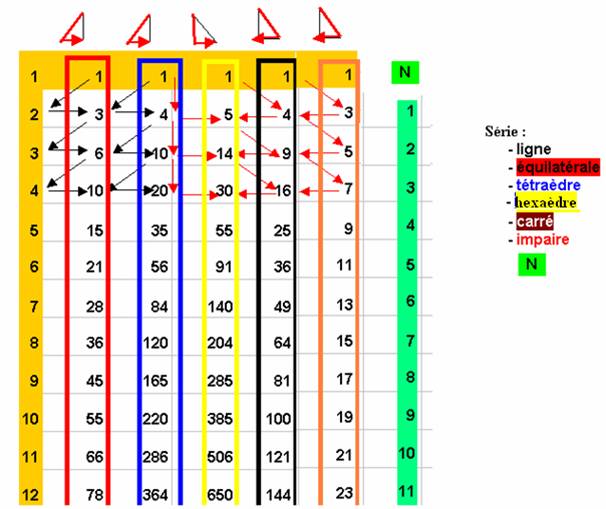
- En empilant des billes je construis une pyramide à base triangle (à 12 étages dans mon exemple) :
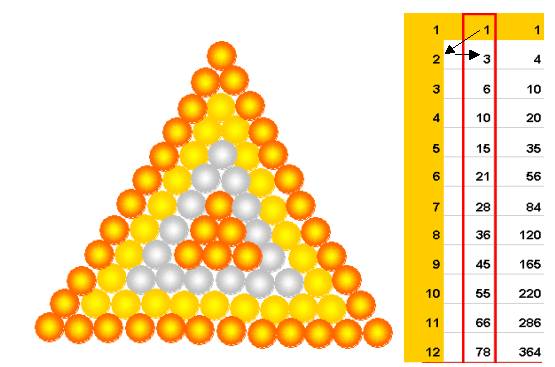
La somme successive des billes dans les lignes se calcule
par tableau d’addition dans la colonne rouge :
La série 1, 2 , 3 , 4 … peut être appelée « série ligne » : c’est le nombre de billes dans chaque ligne, ainsi que le nom de la ligne
La série 1, 3 , 6, 10… correspond à
la surface d’un triangle équilatéral, à une couche triangle , je l’appelle « série
équilatérale »
(ainsi la couche qui contient 12 lignes est formée de 78 billes)
Je peux empiler des couches pour construire la pyramide à 12 étages :
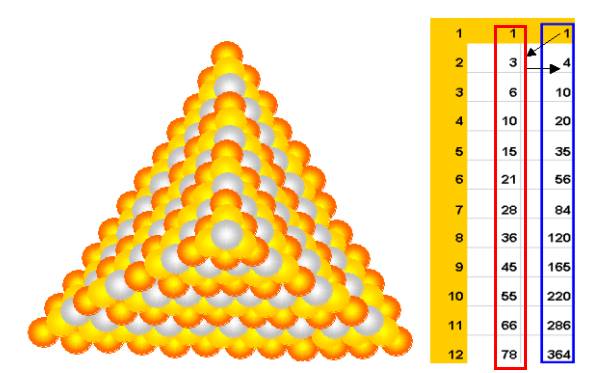
Les nombres calculés dans la colonne rouge sont les nombres de billes dans chaque couche , je peux calculer la somme des couches .
Elle se calcule dans la colonne bleue
La série 1, 4, 10, 20, 35… est le volume en billes de la pyramide qui est un tétraèdre : c’est la « série tétraèdre »
La pyramide à 12 couches est formée de 364 billes.
- L’empilement-billes qui construit la pyramide à base carrée , n’a pas la même structure . Les billes n’ont pas le même contact :
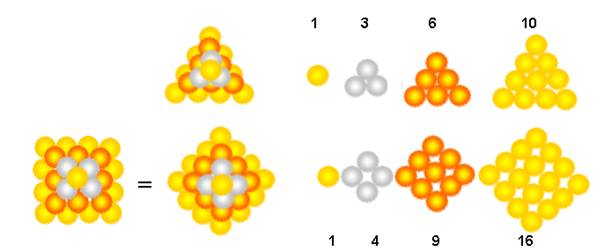
Le nombre de billes dans chaque couche est « la série carrée » : 1, 4, 9, 16,… carré du coté
- Au
lieu d’empiler des billes, on empile des cubes :
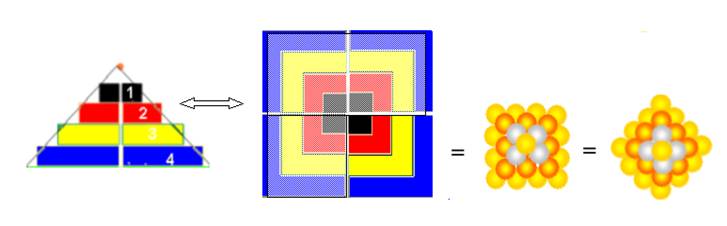
On construit la série carrée avec un quart de la grande pyramide
Avec des cubes on peut construire un autre « carré » qui montre les séries ci-dessous :
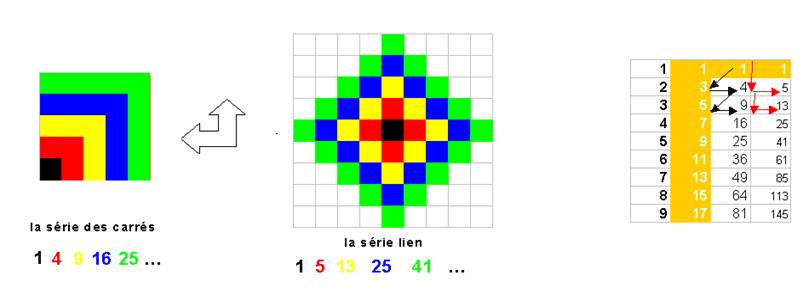
On remarque qu’il existe un « carré
losange » qui n’est pas le carré 5x5 de départ., ses lignes
horizontales forment la « série impaire » :1, 3, 5, 7, 9….
Il permet de construire une pyramide ( on peut la voir en vue de dessus dans la représentation « carré-losange ») : ses couches constituent la « série lien » : 1, 5, 13, 25, 41… qui se calcule par relation d’addition à partir de la série carrée.
(Cette pyramide ressemblerait davantage au premier coup
d’œil à la pyramide carrée en billes, mais elle est parfaitement compacte )
Relation
entre pyramides carrée et triangle
- La pyramide carrée
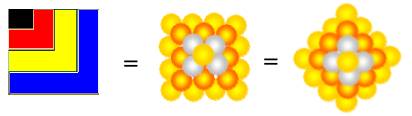
Le volume en billes ou cubes (pour le quart) est donné par le tableau d’addition : colonne jaune
Exemple : 30 billes pour une pyramide carré à base 4x4
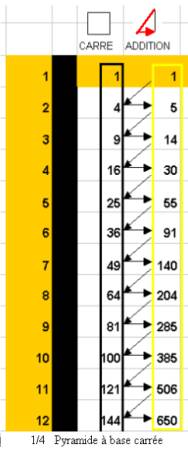
- La pyramide à base triangle équilatéral, est un tétraèdre
A partir de cette pyramide, je construis une bipyramide : c’est un « hexaèdre » (6 faces)
On peut construire une relation d’addition qui donne encore la colonne jaune :
Ce tableau d’addition permet de calculer le nombre de billes de l’hexaèdre, comme somme de 2 pyramides
Exemple : un hexaèdre à base 4, est la somme d’une pyramide à 3 couches et d’une pyramide à 4 couches : Il contient 10 + 20 = 30 billes

La colonne jaune représente le volume en billes des hexaèdres successifs que l’on peut construire ( l’hexaèdre 12 contient 650 billes)
On remarque que le volume de l’hexaèdre (bipyramide triangle) est égal au volume de la pyramide carrée.
Ce volume (colonne jaune) donne la série de la somme des carrés , c’est la « série hexaèdre »
- Relation entre les séries de nombres
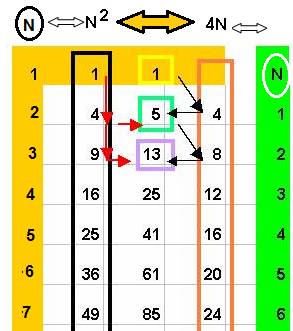
A partir de la série des carrés, on arrive à la série 4N = 4(1,2,3,….. N), ou réciproquement
La « série lien », qui commence par 1, 5 ,13 … est en relation avec la structure de réciprocité 4 du nombre
La relation s’établit entre 2 séries N décalées.
( Ce décalage se retrouve dans une autre construction de la numération que je découvre plus tard, elle fait correspondre alors la série des carrés et la série 6N)
Remarque :
Le lien des 2 séries décalées se traduit par une relation intéressante : (ici représentée pour N=6)
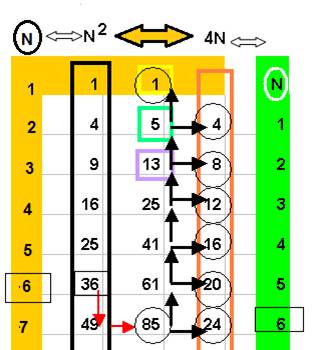
par les dissociations successives :
(n+1)2 + n2
= 1 + 4 ( 1+2+3+4+5+… n )
(ici 72 + 62
= 1 + 4 (1+2+3+4+5+6) )
ou
n2
+2n+1+ n2 –1= 4( 1+2+3+4+5+… n )
( 1+2+3+4+5+… n )
= n(n+1) / 2
( Pour démontrer la
relation mathématique ci-dessus, on a eu
besoin d’être dans 2 niveaux à la
fois ! : c’est la présence au
« Relatif Absolu »
Le relatif absolu prend en compte l’existence de l’absolu et du relatif en même temps : l’existence d’un double zéro à l’origine.)
- la série impaire
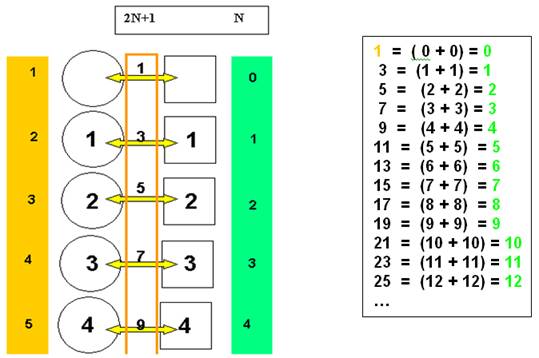
Un nombre impair est de la forme 2N +1 :
On peut voir 1 comme le lien d’une paire 2N qui correspondrait à 2 visions différentes .
Je schématise ces 2 visions ci-dessous, par le cercle et le carré ( ou la bille et le cube) :
Ainsi par
exemple pour N
= 2 5 = 2
+ 1 + 2
Je peux alors même l’écrire sous la forme d’un COUPLE de 2 réciproques liés :
5 = 2
+ 1 + 2 =
( 2 + 2 )
Le nombre N dans sa complétude est ce
Couple : 5 = 2
+ 1 + 2 =
( 2 + 2 ) = 2
![]()
On obtient un résultat qui est fondamental et qui semble tout à fait paradoxal :
Les nombres impairs sont des
paires
Chaque paire peut aussi s’écrire comme un nombre pair , quand on « oublie » le lien de la paire ou son contenant.
C’est je l’ai montré , le cas dans notre arithmétique qui ne tient pas compte du « Grand Contenant »

La suite des nombres se dissocie
en suite paire et suite impaire
Cette « double vision » était décrite dans « nature et représentation du nombre » sous une autre forme :
Le lien entre 2 visions est considéré comme le contenant qui les inclut : ci-dessous il est représenté par le point noir.
Les 2 visions « opposées » ou réciproques, sont le nombre vu comme symbole- nom, un ou « continu » et le nombre « quantifié »ou divisé en points.
Le contenant lui-même fait partie de la totalité ( il ne faut pas l’oublier !) , et c’est ce nombre-contenant qui par le signe = montre son contenu double à l’intérieur de la parenthèse :
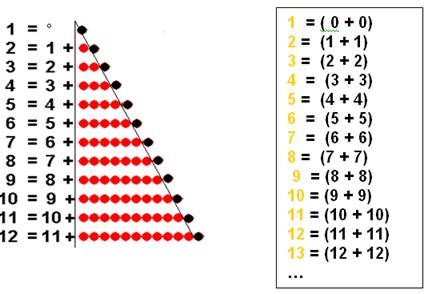
Le
lien contenant-contenu s’exprime par la réciprocité de 4 suites
numériques :
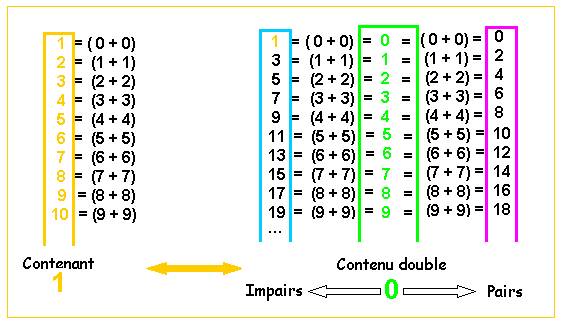
L’ écriture, ci-dessus, nous semble fort étrange…
et pourtant déjà nous connaissons
- la suite de Fibonacci établie par 1 = 0 + 0
- le système de numération que nous utilisons tous les jours basé sur 2 = 1 + 1
- 3 = 2+2 = 4 a permis à Einstein de construire l’Espace-Temps à 4 dimensions
- 4
= 3 + 3 unité de réciprocité sera une illustration de la parité Matrice-Eclaireur , établie par la théorie de réciprocité 4 , qui fera de 6 (parité de 3) sa nouvelle unité
le nombre
@) a permis de définir
cette unité 6
On remarque dans le tableau
ci-dessus, que les 4 suites réciproques, correspondent à 3 couples identiques,
ou « vision 6 » de la même unité : la suite 0,1,2,3,4,5….
Ce lien Matrice-Eclaireur est cause ( ou conséquence ) de
la différence de structure des 2 types de pyramides : c’est ce que
montre le chapitre suivant