Synthèse :
Les nombres premiers et l’origine de la structure numérique 0,1,2,3,4,5,…..
Résultat : (illustré puis expliqué ci-dessous)
La série numérique que nous utilisons , correspond à 2 structures cohérentes décalées par la nature double du zéro Origine .
-La première est basée sur l’unité 6.
-La deuxième met en cohérence le nombre et son carré :
J’explique pas à pas la construction ci-dessus : (des liens permettront de se reporter si besoin aux chapitres de mon étude, qui ont conduit à ces résultats.)
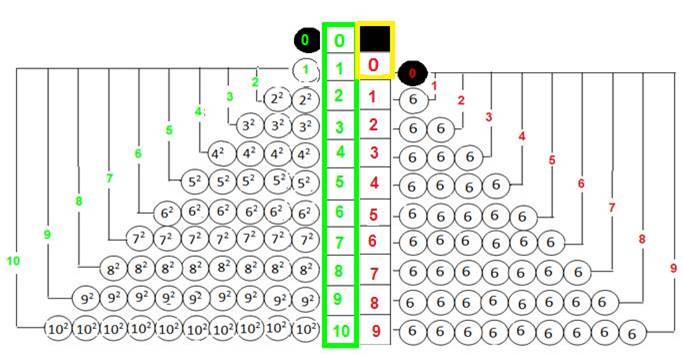
1. Les nombres sont construits avec une unité 6 :
Cette unité que j’appellerai 1 est représentée dans le schéma suivant par la dimension de 6 carreaux), 2 par 2 unités =12 carreaux… : c’est la représentation usuelle que nous avons des nombres :
![]()
![]()
2. Dans la suite numérique, chacun des nombres inclut le précédent, ou s’ajoute au précédent (comme une longueur de corde) :
Je représente, ci-dessous, « la corde » qui ajoute les nombres en série :
La corde aura « un bout », matérialisé par la longueur 0 ,( la plus petite longueur qui correspond à la dimension 1 du carreau)
L’extrémité du bout est l’Origine (point de départ sans dimension)
- La longueur de la corde tiendra compte d’abord de la longueur du bout:
J’obtiens alors la série 0,7,19,37,61…par addition des longueurs, qui représentent les nombres 0,1,2,3,4…

- Puis on tient compte aussi de l’extrémité , de la façon suivante :
L’étude des couches spdf des atomes m’a amenée à considérer une deuxième somme-inclusion ( c’est ce que j’ai appelé « superposition » :
Cette somme est un deuxième niveau où chacun des nombres de la série 0,7,19,37,61… obtenu ci-dessus s’ajoute au précédent : comme au premier niveau, le zéro ( « origine sans dimension »,ici), est compté « 1 »)
Par cette deuxième addition , j’obtiens la série 1, 8, 27, 64, 125… que je reconnais comme la série des cubes ou puissances 3 des nombres 1, 2, 3, 4, 5…
Ces 2 sommes-inclusion sont représentées sur le schéma :
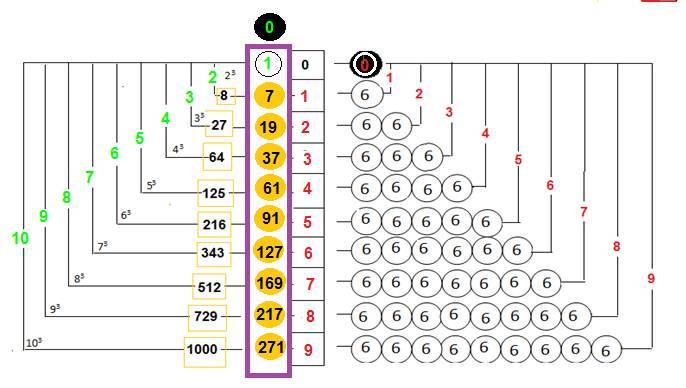
J’ai écrit ensuite les puissances 3, en somme de puissance 2, pour obtenir la beauté-cohérence du schéma de présentation , au début de la page :(je le reproduis ci-dessous.).
(la cohérence exigera que 2 (23= 2x22= 8) corresponde au 1 qui était défini au départ, comme unité 6 ) :
Donc 2 = 1 et 1 = 6

On obtient donc 2 séries décalées ,
je pourrais cependant les appeler : série N2 et série 6N .
J’avais
trouvé de même la relation de la série N2 et de la série 4N
Par l’intermédiaire de la série carrée, il y aura la relation série 4N /série 6N qui est Cause de la relation importante MATRICE-4/ECLAIREUR-6
Le décalage met en évidence l’existence de
2 origines :
Je pourrais
parler ici d’une origine Absolue, et
une origine relative.
Je les ai respectivement représentées par le « point de départ » de la corde et par l’extrémité matérielle ou « bout » de la corde.
Il semblerait que les nombres existent par leur carré dans la structure d’origine absolue, et sont représentés par l’unité 6 dans la structure relative.
(Les 2 possibilités existent à la fois dans un niveau « intermédiaire », ou plus complet puisque pour nous il paraitra comme la présence de l’Absolu dans notre Relatif.
J’appellerai ce niveau nouveau : « le Relatif Absolu », étudié dans un prochain chapitre)
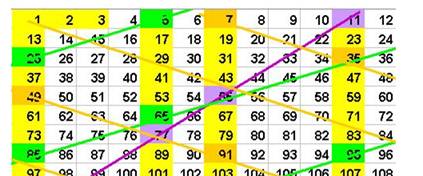
3. Cette corde s’enroule sur une boucle à 12 points, à partir de l’origine « Absolue » (représentée par 0). (les nombres dans cet enroulement 12, ont fait apparaitre les nombres premiers)
Cet enroulement peut se faire dans les 2 sens.
L’origine 0 , que j’ai appelée « relative », existe donc dans les 2 sens, elle est double..
La distance entre chaque point, correspond à la distance « 1 » :
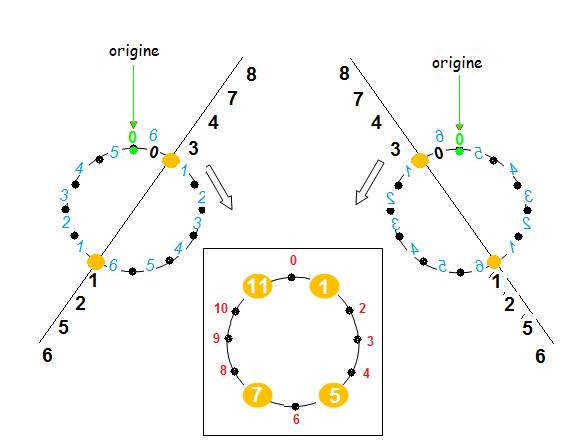
Les nombres de la série numérique, que nous avons décrits ci-dessus : 1,2,3,4,5… se retrouvent, en 4 positions de la boucle.
A partir de l’origine 0, ces 4 positions
peuvent être repérées « de façon familière » par les nombres (1 ,5 ,7 ,11).
Ces positions sont les positions premières et définissent ce que j’appelle le « quaternion premier » : (1 ,5 ,7 ,11)
4. Le « quaternion premier » : (1,5,7,11) , permet de trouver les « nombres premiers » : (rappel du tableau obtenu ci-dessous)
Si on
enroule nos nombres sur « la
boucle à 12 points », les positions (1,5,7,11) contiennent les nombres premiers .
Ils se répartissent ainsi dans 4 colonnes :