Un Cercle …Infini ?
… image du « nombre dans la réciprocité 4 » , le Nombre dans sa complétude serait contenu dans un cercle…
Il est tentant d’essayer de calculer son périmètre et son diamètre pour en déduire une valeur de π :
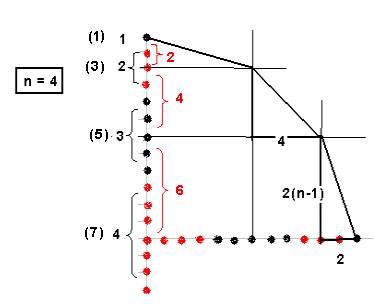
Calcul du quart du périmètre contenant le
nombre n :
C’est la somme des hypoténuses des triangles rectangles
J’ai tracé la figure pour la valeur n= 4
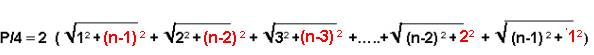
Je remarque que chacun des termes est hypoténuse d’un triangle rectangle dont la somme des cotés perpendiculaire est toujours égale à n
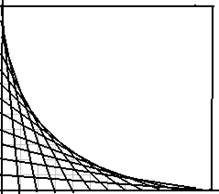
Je représente chacun de ces termes et vois se former un quart de cercle de rayon n, porté par les hypoténuses , inscrit dans un carré de coté n
Si je calcule le rayon du cercle à partir du premier graphique : R = 2( 1 + 2 + 3 +…. + (n-1)) =2 x n (n-1)/2 = n(n-1)
(La formule de la somme ( 1 + 2 + 3 +…. +n ) = n (n+1)/2 est montrée par la structure des Pyramides)
- la valeur du périmètre est « connue » P = 2πR (π apparaît dans la relation périmètre-rayon )
Je calcule ici P/4 x 2/R = π … ( en faisant apparaître le produit par 4 : coefficient de réciprocité, au numérateur et au dénominateur )
( je cherche à calculer la valeur de p)
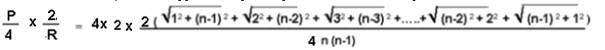
Je trouve la formule belle, car je peux lui donner un sens :
-
Au numérateur je vois
Le numérateur représente donc 2 cercles inscrits dans 2 carrés de coté 2n
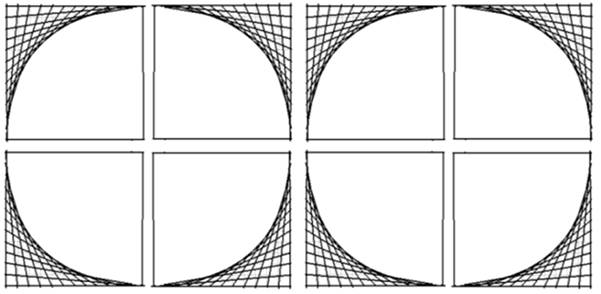
- Le dénominateur est le quadruple produit n (n-1)
Le produit n(n-1) est la surface d’un carré de coté n… auquel il manque …1 coté de longueur n !
(Je considère en effet que c’est un
rectangle n x (n-1) , qui n’est pas tout
à fait carré, il manque à la longueur d’un coté, la longueur 1-minimum de « l’épaisseur du trait », sur toute la
longueur n-maximum de la valeur nombre (dans sa complétude infinie)
qui m’intéresse ici.
L’étude des nombres a montré que les chiffres que nous utilisons ne tiennent pas compte de l’Origine « ZERO », et qu’ainsi il y a un décalage : n est alors n-1
La formule n( n-1) contient les 2 formes.
Il est important de voir que tout le raisonnement ici se fait dans une pensée qui concerne les extrêmes : c’est là que réside le mystère de l’Origine.
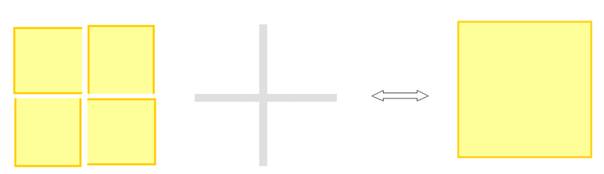
Les 4 carrés (auquels il manque un côté) s’unissent en offrant un coté à un voisin, et recevant un coté d’un autre, pour former le carré de coté 2n dans lequel est inscrit le cercle de rayon n..

L’union des 4 carrés est la « mathématisation » de
la réciprocité 4, la base de la « Théorie de
-
Comment s’établit cette union ?
Toute la subtilité et le mystère de l’Origine sont
contenus dans cette union :
Il ne s’agit pas simplement d’ajouter , ce qui donnerait un carré de coté 2n-1 : il existe ici ce que je pourrais appeler un « partage dans la réciprocité don-acceptation » : le coté manquant, est reçu comme une addition qui n’enlève rien au donneur .
Le lien réciproque apparaît comme un plus gratuit et c’est d’ailleurs ce que par une belle coïncidence du symbole , se dessine dans la représentation du lien réciproque des 4 quarts :
Le lien entre les
- Comment se manifeste l’Origine ?
Pour le cercle que j’étudie, qui contient la complétude du nombre je cherche la relation entre périmètre et rayon .
Au niveau de cet infini la relation entre périmètre et rayon P / R = 2π traduirait simplement la nature de boucle infinie de l’Origine dont j’ai présenté la logique de principe ZERO :
Je le dessine
ci-dessous et en décris le principe :
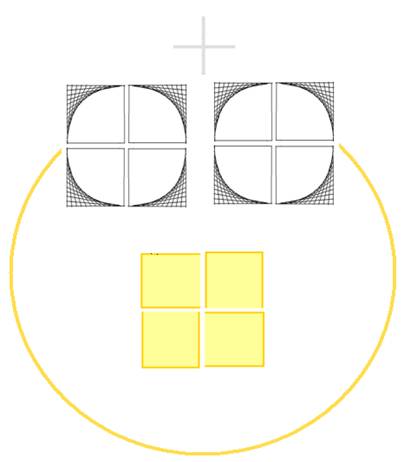
Les 2 cercles sont
les 2 extrémités
de l’Origine Cercle qu’ils créent en s’unissant. Ils sont eux même cette
origine, par leur somme formée des « 8
premiers »
Les 8 premiers (qui sont une constante dans mon travail, sous des formes différentes) sont ici les 8 carrés de coté n, qui par la fermeture qui fait exister la boucle et les fait disparaître, donne naissance à la réalité des 2 faces du carré de coté 2n.
Ceci est le Principe ZERO de la Boucle Cercle ou « Principe π Unique» qui est cause ou source de la réciprocité, de la réversibilité Origine … (il n’y aurait alors pas de second principe…)
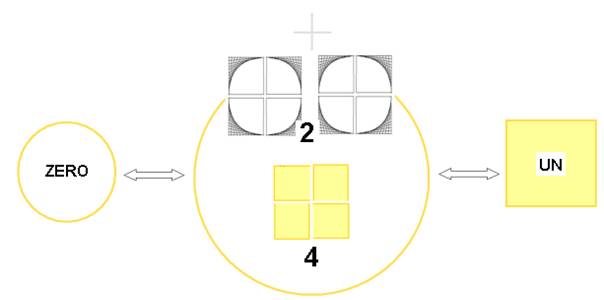
- 2 traduit la parité de l’Origine manquante, qui disparaît à la fermeture de la boucle.
Cette fermeture est paradoxalement création de l’Origine comme boucle Unique : le Cercle.
(J’ai pu aussi parler d’existence paradoxale du cercle : c’est le principe ZERO de la Boucle)
Cette Origine se manifeste dans la réciprocité du ZERO et du UN qui naissent de cette disparition-mutation
- p exprime« l’Originalité » ou principe ZERO
de l’Origine-Cercle dans la
réversibilité de son « Manque-Existence »
C’est ce que l’on appelle « transcendance de p »
On a alors l’existence de la boucle vide , que l’on peut appeler ZERO, et celle du carré-surface UN
La boucle a un rayon n, et le carré un coté 2n
J’ai calculé ci-dessus d’une autre façon le rayon n du cercle R = n(n-1)
Quelle est la condition telle que n = n(n-1) n2-2n=0 ? n=
0 n = 2
Le cercle étant celui qui contient par construction le nombre
n, cette double condition définit le Cercle
centré de rayon 2:
c’est donc le Cercle Origine Grand Contenant du
Nombre 2 et son Centre Origine 0.
![]()
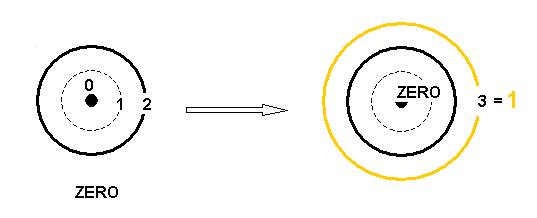
Si le cercle de rayon 2 est l’Origine ZERO, le
cercle de rayon 3 est le départ 1)
Le cercle de rayon 1, est inclus dans cette boucle Origine qui est le ZERO dans sa totalité .
On remarque alors que la condition qui définit le transfini : n +1= n est s’écrit - pour n=0 0 + 1 = 0 1 = 0
n=1 1 + 1 = 1 (avec 0 = 1) ou 2 = 1
n=2 2 + 1 = 2 3 = 2 =1
… par suite tous les nombres sont définis comme transfinis : c’est ce que j’ai appelé « le nombre dans sa complétude »
·
A notre niveau du fini mathématique , 2π apparaît comme la relation de rayon à périmètre :
A partir de « ma belle formule » je me suis acharnée à vouloir calculer π … malgré tous mes efforts de tableur… je n’y arrive pas… et il m’a fallu du temps pour me rendre compte que je n’étais plus dans la vision classique mathématique, mais dans la dimension extrême de l’Origine à la fois infinie et nulle et toujours UNE. Celle de la « méta-mathématique »
Je comprenais ainsi le sens de
« Transfini » ou de l ’adjectif « transcendant » que l’on
donne à π : « nombre
transcendant »
Ainsi… 2 comme π ou 0 étaient aussi 1… !
Pour ma part je n’avais donc pas à redonner une méthode de calcul de π , je devais traduire clairement, de façon purement mathématique, la vision nouvelle que j’en avais au niveau métamathématique
Celle-ci s’exprime de plusieurs façons :
· Dans la vision métamathématique :
- Les 2 extrémités d’un rayon ferment la boucle π … le Cercle existe dans la magie étrange de cette rencontre, c’est ce qu’exprime aussi le Cœur de la Fleur d’Or :
C’est la magie d’une rencontre qui crée le 3…au cœur d’une boucle qui se ferme dans la paradoxale Existence du Cercle !
Le rayon serait alors 0 et le périmètre l’infini .
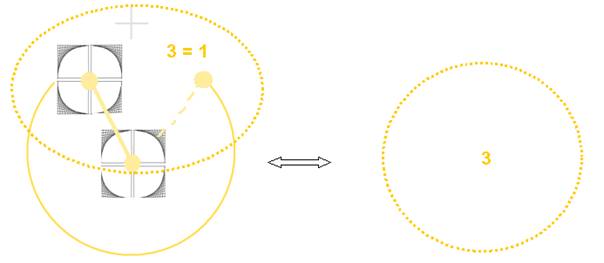
La valeur transcendante de π, est alors le rapport mathématique non
défini qui pourrait s’exprimer
par π
= ∞/ 0 = 3
C’est cette valeur 3 qui a pu être reconnue comme la « Trinité » mystique. Elle appartient à une réalité qui n’est pas mathématique mais « méta-mathématique »
La valeur mathématique de π
dans la beauté de son incomplétude infinie 3,1416… traduit
« l’impossibilité » de la représentation de
- Voici pourtant un autre essai de représentation , dans une autre vision métamathématique :
le rayon infini reviendrait à sa source pour former lui même le cercle infini
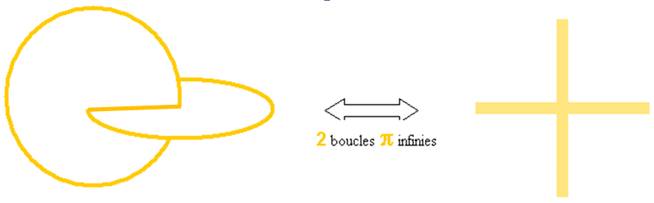
Le périmètre et son rayon existent dans une parité réversible qui est celle de 2 « réciproques perpendiculaires » : 2π traduit cette vision métamathématique de 2 « boucles π »
Remarque : Champ électrique et champ magnétique sont 2 réciproques perpendiculaires de la réalité physique.
« La réciprocité perpendiculaire » est la première notion de réciprocité que j’ai rencontrée et introduite dans mon travail.
La réalité mathématique du produit vectoriel est une
traduction de
La vision symbole du signe + , n’est autre alors dans cette complétude du 3 que la représentation mathématique de notre système orthonormé et de son Origine
Je reviens donc au point de départ ?… rien de nouveau … ?
…ou une
confirmation de
-
Mais où se trouve l’Origine ?
Je devais poursuivre avec de nouvelles questions :
Dois-je tenir compte du Zéro ? Où se trouve l’Origine ?
Comment tenir compte de l’infinité d’imbrication dans la complétude du nombre ?…
Je devais utiliser ma belle formule mathématique…
C’est l’objet du prochain chapitre