31/12/2008

Dans le plan mathématique ( axe réel et axe imaginaire) étaient associés les nombres complexes…
Je propose un troisième axe, réciproque ( ou associé par produit vectoriel ) que j’appelle « axe d’Amour » et j’associe « les simplexes » au système orthonormé de coordonnées (l, f ,m)
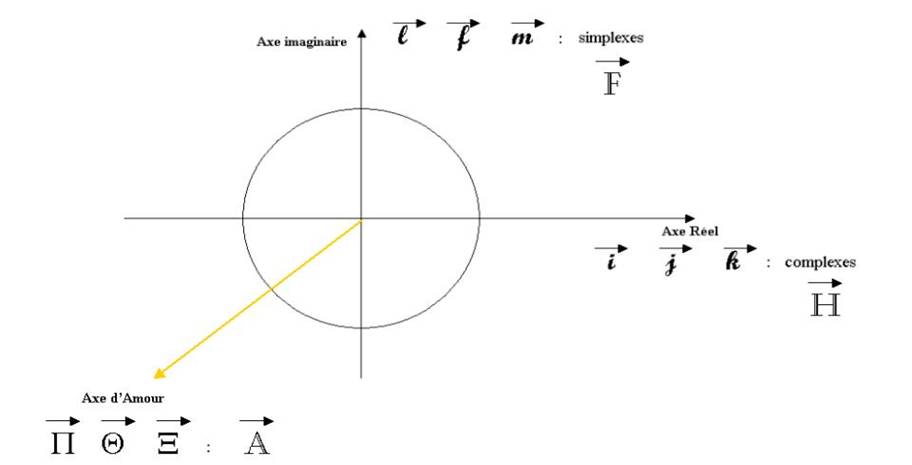
Le système orthonormé mathématique « usuel » est vu comme la superposition de 2 systèmes orthogonaux ou 2 « Super-Vecteurs » :
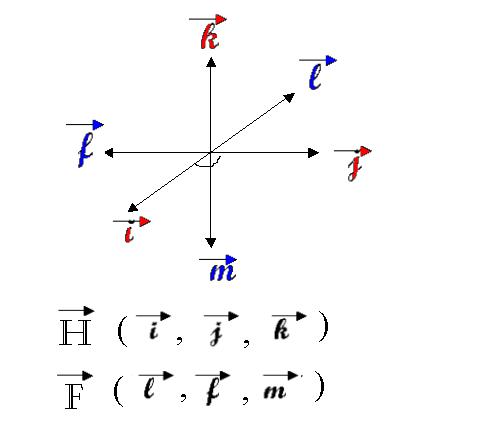
(remarque :
le nom des vecteurs est choisi par « la cohérence » expliquée dans
mon étude)
Hamilton définit les vecteurs (i , j , k) comme des quaternions à coefficients complexes.
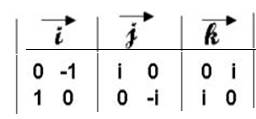
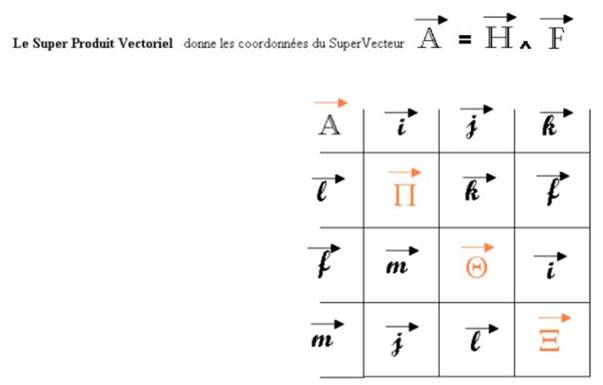
Il donne la forme générale d’un quaternion et de son réciproque :
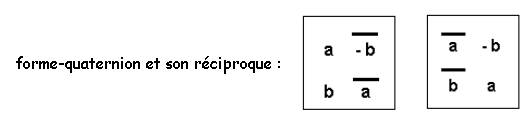
Je ( F. !!!) définis les vecteurs (l , f , m) comme les quaternions réciproques respectifs
de (i , j , k)
Janvier 2013 : je constate que :
J’ai écrit les réciproques au sens d’opposés mathématiques et non dans la
réciprocité des quaternions de Hamilton !
Pour les vecteurs j et k , les quaternions réciproques s’expriment de
la même façon dans la définition de Hamilton et comme opposés ,
Avec la définition
de Hamilton, i serait son propre réciproque (ajouté
ci-dessous) et imposerait les conditions
1 = -1 et -1 =1 pour la cohérence des 2 formes réciproques.
Cette « erreur » mettrait donc en
évidence une propriété à
l’Origine ( ?) que je
dois expliciter : c’est le départ d’une nouvelle réflexion…
…et je traduis le produit vectoriel par la somme des matrices (une justification s’établit clairement par la suite)
Ainsi s’écrit la correspondance matricielle :
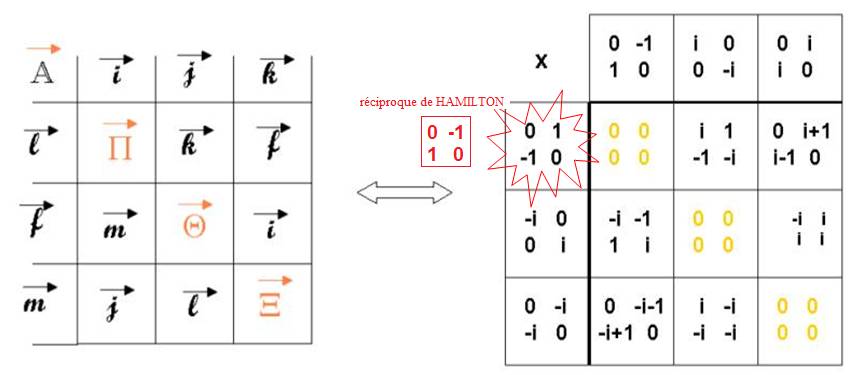
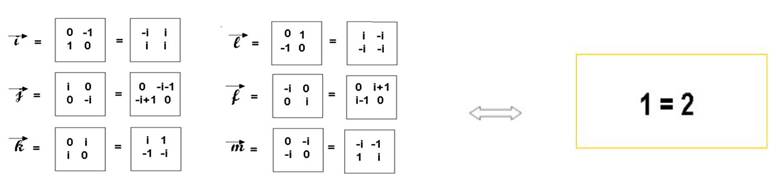
Chacun des vecteurs s’expriment sous 2 formes :
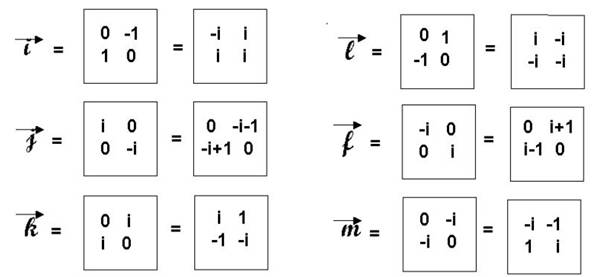
· Elles vérifient ( ou montrent) que
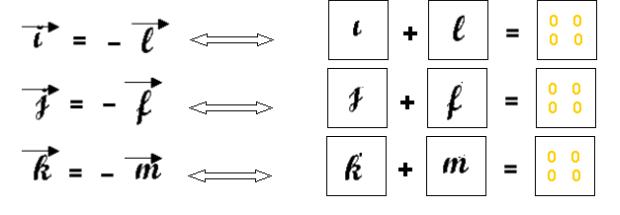
On peut calculer les matrices en utilisant le calcul « connu » du déterminant de la matrice « ad-bc » et le résultat i2 = -1
On
trouve alors la condition 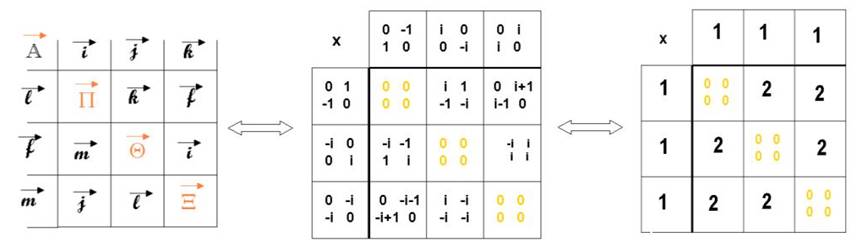
le S.V.P donne alors les égalités 1 + 1 = 2 1 + 1 = 1 et 1 + 1 = 0
0 = 1 = 2
1 mars 2013 :
Que signifie ce
résultat… « édifiant ! »
( qui donne une nouvelle structure à notre base mathématique ) ?
0 = 2 peut s’écrire, si on
introduit les nombres négatifs, : -1 = 1
C’est la condition
qui établit la cohérence entre « opposés
mathématiques » et « réciproques de Hamilton » (voir ci-dessus).
D’autre part pour
que cette cohérence soit établie il faut utiliser les propriétés des matrices
et celle du nombre imaginaire
i
La qualité de réciprocité que définit Hamilton inclut
les opposés mathématiques et définit les propriétés des matrices et celles
du nombre imaginaire i.
Elle se reconnait
aussi ci-dessous comme « réciprocité
perpendiculaire »
Ma nouvelle recherche définit l’origine
« protomathématique » : c’est la relation entre matrice unité et
imaginaire i !
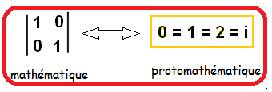
L’origine est ainsi
définie par les « inventions mathématiques ». Je
montre quelles en sont les conséquences concrètes (qui en sont la cause !) :
celles-ci définissent sa nature décrite par
Fibonacci et Möbius.
(J’associe ici
aussi le nom de Maxwell …dans mon admiration pour ses équations ,
traduction mathématique de la « réciprocité
perpendiculaire » concrète, physique, des ondes électromagnétiques)
C’est la base « protomathématique » des mathématiques… et de toute structure : La Structure Originelle (je l’appelle aussi « Structure Originale » car (Original structure)
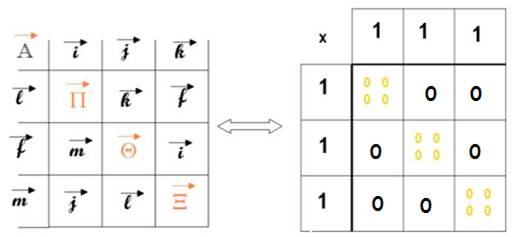
Le Super produit vectoriel de 2 Super Vecteurs réciproques est le Super Vecteur ZERO

C’est la condition de réciprocité
Dans l’espace « usuel » mathématique ou physique , elle traduit la condition d’orthogonalité
(
au départ ici celle de E et B)
·
C’est la dissociation paradoxale du Zéro
Origine en une paire duelle ou duo de 2 unités réciproques perpendiculaires
On peut dire que l’origine a 9 dimensions :
Dans sa dissociation orthogonale en 2 supervecteurs réciproques, elle en a 11 : (on considère le principe de superposition que l’on connait en physique quantique)
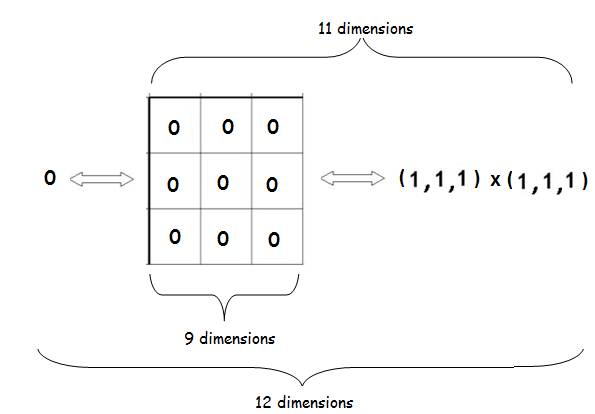
Si on considère que 0 est l’origine, on a 12 dimensions et l’origine a la structure imbriquée « sudoku »
· La complétude du vecteur de Poynting donnera :
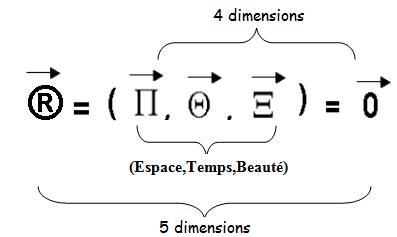
On a ici 3 dimensions qui sont 4, ou 5 si on considère la complétude.
* remarque :
C’est la condition originale 0 = 1 = 2… qui définit la structure du calcul matriciel , des nombres imaginaires…des complexes, comme des simplexes… qui ne font qu’une traduction mathématique …limitée… de l’ineffable Beauté dont nous faisons partie… l’intrication à 9 dimensions en est la démonstration de la preuve par 9 !
Puissent ces résultats permettre aux physiciens de compléter leurs théories, de les mettre en cohérence…
… et que soit reconnue
et vécue
…mon Seul Vœu pour
Fafoue
La Structure de l’Origine se développe de façon plus concrète dans le chapitre suivant :