20/08/16
La conjecture de
Goldbach
« Tout nombre entier pair supérieur à 3 peut s’écrire comme la somme de deux nombres premiers. »
Le chapitre précédent a montré l’origine de notre numération, en élargissant notre vision « relative »…
La conjoncture utilise des termes qui nous semblent évidents.
Ils sont basés sur des concepts mathématiques que notre habitude nous empêche de remettre en cause.
Je les redéfinis à partir d’une vision nouvelle :
Qu’est ce qu’un nombre ?
Qu’est ce qu’un nombre pair ?
Qu’est ce qu’un nombre premier ?
Qu’est ce qu’une somme ?
A partir de cette
« vision originale » ou « original vision », j’en ferai une démonstration « première » ou protomathématique.
C’est la présentation originale des résultats de l’étude protomathématique que j’ai développée dans mes chapitres .
o
Un NOMBRE
Le nombre peut être vu comme un contenant avec son contenu.
Exemple :
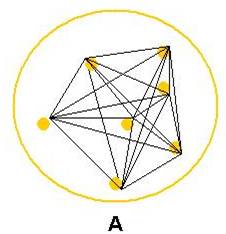
Dans leur contenant les points sont
liés par des relations que je symbolise ici par des segments
Ici, par exemple, pour 7 points,
chacun se lie aux autres et établit 6 relations
Chaque point d’un nombre n établira
ainsi (n-1) relations avec les autres
Il y a donc 7 x 6 = 42 relations
entre les 7 points ou plus généralement n(n-1) relations
Sur le schéma on n’en voit que la
moitié !… car ces relations sont doubles : ce sont des
relations réciproques
Il est en mathématique , une formule
qui donne le nombre de « combinaisons » entre n points 2 à 2 :
C2n= n(n-1)/2 elle donne
le nombre des traits visibles de la figure (ici 21= 7x6/2 )
La nature de réciprocité du lien est
supprimée par cette division par 2.
Pour le nombre A ci dessus il y a a (a-1)
relations = (a2 –a) et
a points dans le contenant
La représentation symbolique du Nombre peut alors prendre une autre forme :
- Le nombre de liens dans A est (a2 – a)
- La boucle A , contenant est une corde formée par a morceaux
reliés par a nœuds-points
On enlève a points-nœuds-liens des (a2 – a) liens-relations, il en reste a2 dans le contenant, lui même formé par a liens-points
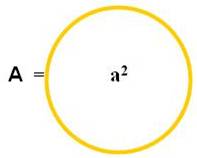
Le nombre A est à la fois représenté par a (contenant)
et par a2 (contenu)
Le choix de nos représentations va construire nos mathématiques et notre vision du monde.
-La Spirale des Nombres
Des
visions différentes peuvent exister en même temps ( nous connaissons cela en
physique, vision classique et quantique ne s’excluent pas)
On peut
voir les nombres enroulés sur une spirale unique :
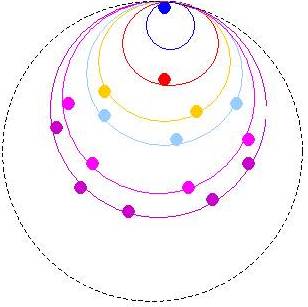
La Corde Unique s’enroule…
Elle va former la suite des nombres…
Après la première boucle à un
morceau, se forme la boucle à 2 morceaux…
Elles se rencontrent en un point… qui
devient le Point UN de la Boucle UN… qui manquait ! C’est le Point
Origine.
La Boucle 2 a 2 points (dont le
point Origine) donc 2-1points =1 point
La Boucle 3 a 3 points (dont le
point Origine) donc 3-1points =2 points
La Boucle 4 a 4 points (dont le point
Origine) donc 4-1points =3 points
…
La Boucle n a n points (dont le
point Origine) donc n-1points
Le point origine est le lien de
chacun des nombres
Le lien commun à chacune des boucles
, semble manquer sur chacune d’elle.
Le
lien apparaitra toujours comme un manque
, je rapprocherais ce lien de l’énergie
de liaison en chimie ( « manque » représenté par le signe
« négatif »)
-Le Nombre comme Boucle
On trouve chaque nombre comme spire de la spirale
Le nombre peut donc être représenté par une boucle
La boucle contient chacun des nombres de la série 1,2,3..N .
La boucle tracée comme « continue », est ainsi « quantifiée » par les nombres –points qui la constituent.
C’est
« la réciprocité
continu-quantifié »
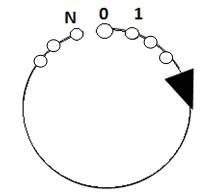
La spirale
établit que la Boucle N, fermée, a N-1
points : c’est donc que les 3
points N ,0, 1 sont confondus (3 en 1)
On peut aussi voir Fin et Commencement , liés au point O-origine, et ce lien les fait disparaitre.
Ce principe est le secret paradoxal de
toute boucle fermée :
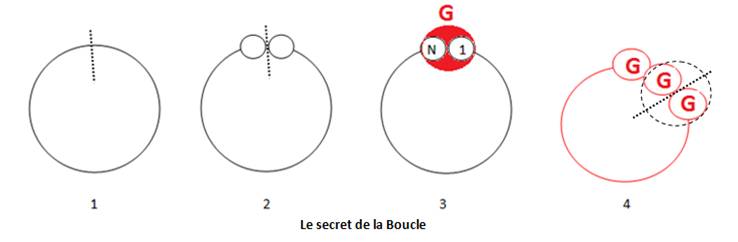
1- boucle fermée
2- Quand on ouvre la boucle 2 points ou 2 extrémités apparaissent.
3- Si on recolle les 2 extrémités par un point « Glue », les extrémités disparaissent.
4- On peut ouvrir la boucle en tout point.
Chaque point de la boucle peut être considéré comme un point Glue G . Ce point G est une paire de points qui se libèrent à l’ouverture.
Problème - paradoxe : comment compter les points de la boucle ? Quelle est la dimension du point ?
La suite de Fibonacci qui s’explique par ce principe, m’a permis de voir le paradoxe du Cercle : la valeur non-finie de p montre que la courbe ne peut être fermée !
La
condition pour que le Cercle se boucle parfaitement, permet d’établir «la théorie de la réciprocité ».
En voici une simple expression :
« Chaque UN est 2, et les deux ne sont qu’UN »
-Les 2 sens
A partir de l’origine, les mathématiques utilisent les nombres positifs et les nombres négatifs
![]()
Pour une boucle, on pourra considérer 2 sens de parcours :
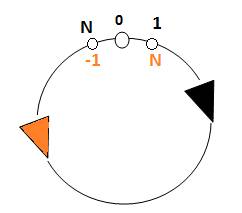
C’est la boucle vue à l’endroit ou à l’envers, ou les 2 à la fois.
Il y aura
ici 5 points confondus (5 en 1).
On peut en
donner une représentation en faisant intervenir ce point unique de retournement :
un TWIST
-« Le TWIST
original »
A l’origine, un point TWIST, qui transforme la boucle en boucle de
Möbius
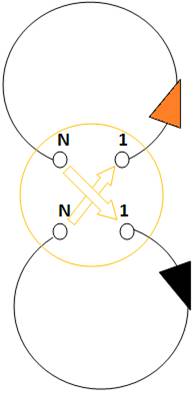
Le double sens est sens unique, mais il peut se voir dans l’autre sens !
cle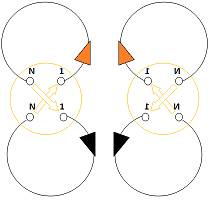
On représente alors une paire de boucles de Möbius.
Remarque : le TWIST peut se voir en tout point de la Boucle . Chaque point peut être considéré comme Origine et Fin.
o
NOMBRE PAIR
-Il est représenté par le symbole 2N, et orienté comme la suite numérique 1,2,3,4…

Quand on utilise les 2 sens :
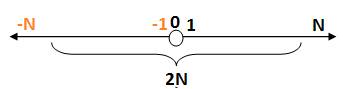
On voit le
nombre 2N , nombre pair, comme « complétude
du nombre N ». Le nombre N est
formé de 2 réciproques inséparables
Utiliser les 2 sens , c’est voir la présence d’un lien invisible qui unit les « réciproques » et permet le changement de sens : c’est le TWIST de l’Origine .
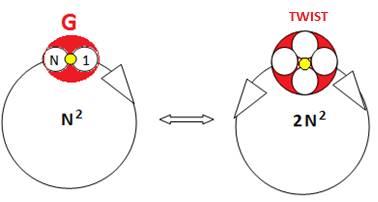
« Le TWIST original » permet de donner la représentation de complétude du Nombre :
2N est
complétude du Nombre N, mais N = 1 (réciprocité continu-quantifié : N confondu à 1 sur la boucle) et N=N2 (réciprocité contenu-contenant) …
o
Nombres premiers
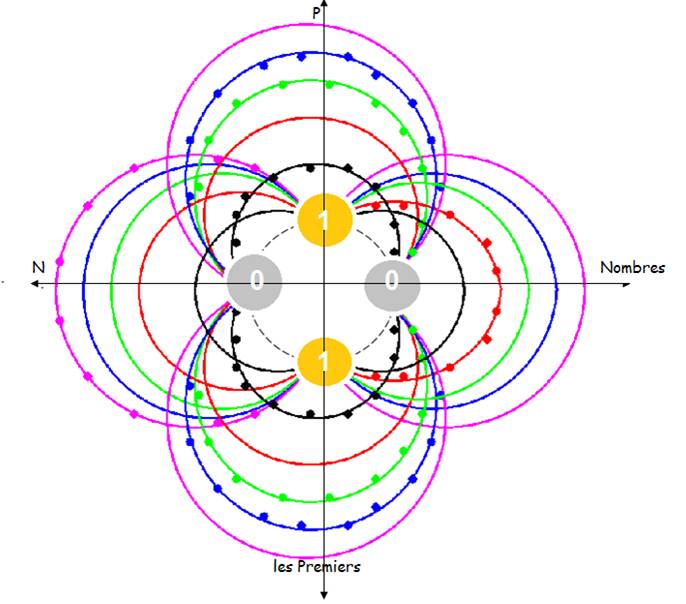
Les nombres premiers sont dévoilés par « le crible paradoxal » de la suite des nombres twists que découvre la théorie de la réciprocité .
Les nombres premiers sont alors vus comme un ensemble de sinusoïdes :
Chacune a une onde réciproque.
La somme de 2 ondes réciproques est « nulle » : les 2 ondes, parcourues en sens inverse, sont
déphasées de p
Les nombres premiers sont alors
représentation de « ZERO »
Les ondes
sont une représentation en mouvement,
dans le temps.
On peut
aussi représenter les nombres premiers par le système des boucles.
Chaque
boucle est « contenant d’une onde première » : diamètre
de la boucle//période de la sinusoïde
Je
ne peux écrire « = »… la
Boucle n’existe que hors du temps !
J’ai montré que le cercle n’est pas une
Boucle dans notre temps, celui des mathématiques . Il est
« protomathématique », antérieur au temps…
La
réciprocité BOUCLE//sinusoïde traduirait
alors la « réciprocité
Espace//Temps »
Ces
« Boucles Premières » , liens qui nous semblent des manques
sont des « boucles-ZERO »
-Si on
considère le nombre pair décrit ci-dessus, il peut être formé Boucle ou fermé en boucle, si on ajoute
2 liens :
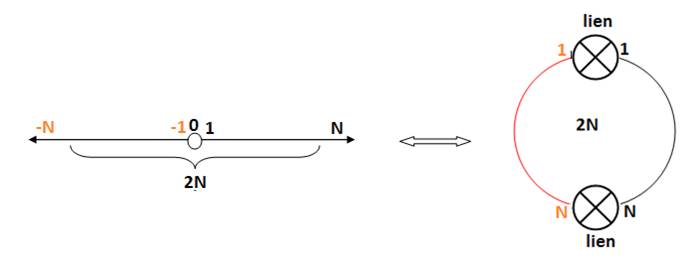
Les liens seront des Boucles Premières :
Ainsi le nombre pair 2N se
forme par le lien avec 2 nombres premiers P :
C’est la
traduction ou démonstration de la
conjecture de Goldbach, au
« niveau premier », celui de
l’Origine
La
somme « + » rencontrée à notre niveau relatif, comme
l’égalité « = » ,
contiennent toute la complétude de l’Origine
qu’elles ne peuvent traduire…
… et paradoxalement c’est tout ce quI fait la
BEAUTE des mathématiques
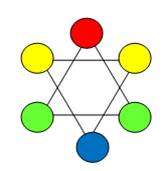
Voici une
« image protomathématique ou magie( !) »,
représentation de la conjecture de Goldbach :
On y
reconnait la complétude du nombre N, ou le nombre pair 2N, formant un lien de réciprocité avec 2 nombres premiers
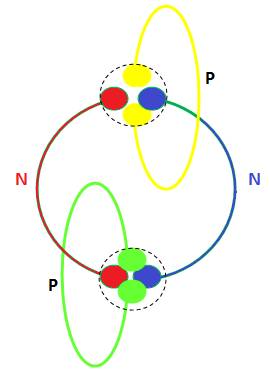
Les couleurs
que j’utilise ici, sont en cohérence avec toute la théorie.
(Le schéma
n’est qu’une autre interprétation de la Cohérence qui s’est construite aussi
avec les parties « métaphysique » et « physique » de la théorie.)
Je peux
représenter ces liens par la forme plus simple de « l’Eclaireur »
-Matrice
et Eclaireur
Dans la
vision de l’origine, « vision originale », nous avons montré
que :
Tout
Nombre N est 1
Tout
Nombre premier P est 0
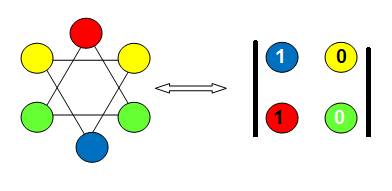
La
conjoncture de Goldbach se justifie dans la
réciprocité Matrice-Eclaireur.
-Le double
réseau
C’est le
lien du Relatif-Absolu :
-nos nombres appartiennent à
notre monde relatif
-les nombres premiers
appartiendraient à l’Origine que j’appelle Absolu
LE LIEN
ORIGINE-Matrice décrit « la
réciprocité perpendiculaire » des
2 réseaux
Réciprocité
perpendiculaire des 2 réseaux Relatif-Absolu
Remarque : j’ai complété un schéma
tracé en 2010 à partir des nombres
twists, mais qui avait évolué si vite dans toute une série de schémas, que je
n’avais pu en retrouver le sens pour rédiger un texte pour un chapitre qui s’appellerait
« générateur-transformateur »
o
Qu’est ce qu’une somme ?
La
Somme « protomathématique » ,
est une somme-inclusion .
J’ai
rencontré cette inclusion : chaque niveau ou couche électronique incluant
les précédents pour expliquer l’intrication des orbitales s,p,d,f des atomes
et l’ai utilisée dans les chapitres
précédents
Cette
inclusion est aussi « superposition » dans le sens quantique du
terme : « tous les états existent à la fois »… et leurs
inclusions s’ajoutent dans la
participation au Tout UN
La Somme
est Complétude
Conséquence :
Il existe un état de complétude que
symbolise ici le TOUT-Nombre = 1 (somme-inclusion
de toutes les boucles nombres : la spirale unique qui est double si l’on considère les positifs
et les négatifs)
Le TOUT-Premier = 0
(somme –inclusion de toutes les Boucles Premières) apparait comme une onde qui manque
: c’est le LIEN
paradoxal du TOUT… avec RIEN … qui ne
peut exister hors du TOUT !...
C’est le paradoxe du GRAND CONTENANT
Il est peut
être difficile de saisir ce dernier
paradoxe, pour moi évident ici .
Le
Grand Contenant qu’oublient les mathématiques était indispensable à la construction protomathématique de « la théorie de la
réciprocité ».
o
QU’EST CE QU’UNE BOUCLE ?
Elle se caractérise par sa paradoxale non
existence dans notre temps… le Cercle n’existe pas comme Boucle (fermée)
Le temps est la destruction de la BOUCLE …
la fin , n’est pas le commencement… car l’évolution crée… de nouveaux états qui
chacun contient TOUT...
Si on ose rencontrer le TEMPS… GRAND
CONTENANT du Tout … alors TOUT est là … pour le jeu et la Joie de l’ESPRIT…
CONCLUSION :
Je pensais avoir enfin bouclé ma Boucle !… je suis presque déçue de démontrer que c’est sans fin …
o Les bonus ou conjectures
-Goldbach et la
physique
La réciprocité perpendiculaire des boucles (ci-dessus) peut être vue comme réciprocité des ondes.
Nous connaissons la réciprocité perpendiculaire de la propagation des ondes électromagnétiques
La réciprocité perpendiculaire des boucles traduit celle des champs électrique et magnétique.
La double
réciprocité perpendiculaire « réciprocité
champs//ondes » est traduite par les équations de Maxwell et a pour modèle celle des nombres : « réciprocité Espace//Temps »
-Goldbach et la chimie
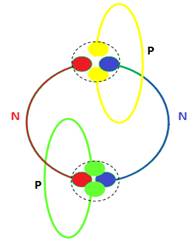
Remarque
: … ! Mes schémas m’amènent
toujours plus loin que ce que j’en attends… ! :
Les
coïncidences de lettres ne sont jamais fortuites, mais j’oserais dire se font
dans une « magie » surprise que je redécouvre toujours avec joie !
C’est
ainsi que je vois une nouvelle représentation de l’atome d’Helium ( 2 protons
et 2 neutrons), le lien se faisant par
les 2 électrons .
Il
resterait à justifier la nature de réciprocité de l’électron dans ce lien
physique … mais « la théorie de la réciprocité » le voit comme
participant d’un quaternion-(unité de réciprocité)
Et , comme
tout
Nombre est une
vision de l’UN, unique et pair, tout
atome est une vision du seul atome He: « L’atome
d’helium est la complétude du quantum-matière »
Le symbole de l’atome apparait sur l’image 2 fois de plus (2P,2N)
Je risque l’hypothèse de cet « Helium du
relatif absolu » :
La figure
représente aussi le lien 3 du relatif
absolu, par 3 atomes d’Helium
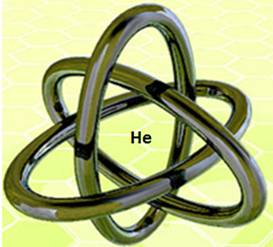
Complétude trine « atome d’He »
Cette
complétude correspond à 3x
(2N,2P) : 6 neutrons, 6 protons, 6 électrons : c’est la structure de l’atome de carbone
-L’importance
de la chimie du carbone et de sa participation à la vie, font du carbone un
élément remarquable dans le tableau de Mendeleïev
-On
remarque aussi 6,6,6 : la théorie de la réciprocité
insiste sur l’unité 6 (représentée par l’éclaireur)
Elle est parité de l’unité trine
3 du relatif-absolu et base
de la construction des nombres twists ou premiers par sa dissociation
paradoxale. (Ici l’unité 6 est elle-même trine)
Une autre
interprétation du tableau de Mendeleïev deviendrait possible, mettant en
évidence des propriétés particulières de certains atomes plus « parfaitement réciproques »
Ainsi par
exemple le carbone tétraédrique s’expliquerait aussi par la relation
Matrice-Eclaireur (4-6) …
Voici
donc, pour un long chapitre qui fait lien (qui
manquait), pour relier
tout… à… sa Cohérence-Beauté…
Inhérente au TOUT, la Beauté de Cohérence est
mise en valeur par les relations de réciprocité et
d’harmonie entre les parties …
Le secret était détenu par les nombres premiers…